已知曲线C:y=x3-3x2,直线l:y=-2x
(1)求曲线C与直线l围成的区域的面积;
(2)求曲线y=x3-3x2(0≤x≤1)与直线l围成的图形绕x轴旋转一周所得的旋转体的体积.
分析:(1)先求出曲线C:y=x3-3x2,直线l:y=-2x的交点坐标,确定出积分区间与被积函数,用积分求出曲线C与直线l围成的区域的面积;
(2)曲线y=x3-3x2(0≤x≤1)与直线l围成的图形绕x轴旋转一周所得的旋转体的体积可由一个圆锥体的体积减去一个不规则几何体的体体积,被积函数为π[(-2x)2-(x3-3x2)2],求出积分即可得到所求的旋转体的体积
解答: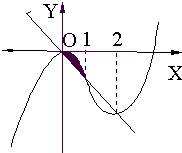
解:(1)联立y=x
3-3x
2与y=-2x得:x=0,1或2.
∴曲线C与直线l有三个交点.
y'=3x
2-6x令y′=0得:x=0或x=2
∵当x∈(-∞,0)∪(2,+∞)时,
y′>0,当x∈(0,2)时,y'<0,
∴曲线C大致形状如图所示.
∴S=
∫[x3-3x2-(-2x)]dx+
∫(-2x-x3+3x2)dx=
(2)由题意,旋转体的体积V=
∫π[(-2x)2-(x3-3x2)2]d x=
π
点评:本题考查用定积分求简单几何体的体积,解着此类问题,关键是掌握积分的几何意义及根据题设条件确定出被积函数与积分区间,熟练掌握求导的运算规则是正确求定积分的知识保证.

 解:(1)联立y=x3-3x2与y=-2x得:x=0,1或2.
解:(1)联立y=x3-3x2与y=-2x得:x=0,1或2.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案