
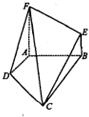
 如图,四边形ABEF和四边形ABCD均是直角梯形,∠FAB=∠DAB=90°,AF=AB=BC=2,AD=1,FA⊥CD.
如图,四边形ABEF和四边形ABCD均是直角梯形,∠FAB=∠DAB=90°,AF=AB=BC=2,AD=1,FA⊥CD.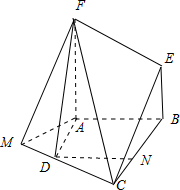 证毕
证毕| 5 |
| AM |
| DN |
| AD |
| CD |
| 1×2 | ||
|
2
| ||
| 5 |
22+(
|
2
| ||
| 5 |
| AM |
| MF |
| ||
| 6 |
| ||
| 6 |


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
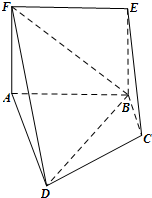 如图,四边形ABCD为直角梯形,AD∥BC,AD⊥CD.AD=AB=2BC,四边形ABEF为矩形,平面ABEF⊥平面ABCD.
如图,四边形ABCD为直角梯形,AD∥BC,AD⊥CD.AD=AB=2BC,四边形ABEF为矩形,平面ABEF⊥平面ABCD.| 1 | 3 |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年上海交大附中高三数学理总复习二空间向量与立体几何练习卷(解析版) 题型:解答题
如图,四边形ABEF和四边形ABCD均是直角梯形,∠FAB=∠DAB=90°,AF=AB=BC=2,AD=1,FA⊥CD.
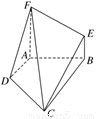
(1)证明:在平面BCE上,一定存在过点C的直线l与直线DF平行;
(2)求二面角FCDA的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
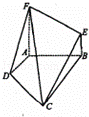
如图,四边形ABEF和四边形ABCD均是直角梯形,∠FAB=∠DAB=90°,AF=AB=BC=2,AD=1,FA⊥CD.
(Ⅰ)证明:在平面EBC上,一定存在过C的直线l与直线FD平行;
(Ⅱ)求二面角F﹣CD﹣A的余弦值.
查看答案和解析>>
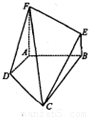
科目:高中数学 来源:2013年安徽省江南十校开年第一考数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com