优生乐园系列答案科目：高中数学 来源： 题型：
2013年9月20日是第25个全国爱牙日。某区卫生部门成立了调查小组，调查 “常吃零食与患龋齿的关系”，对该区六年级800名学生进行检查，按患龋齿和不患龋齿分类，得汇总数据：不常吃零食且不患龋齿的学生有60名，常吃零食但不患龋齿的学生有100名，不常吃零食但患龋齿的学生有140名.
（1）能否在犯错概率不超过0.001的前提下，认为该区学生的常吃零食与患龋齿有关系？
（2）4名区卫生部门的工作人员随机分成两组，每组2人，一组负责数据收集，另一组负责数据处理.求工作人员甲分到负责收集数据组，工作人员乙分到负责数据处理组的概率.
附：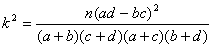
|
| 0.010 | 0.005 | 0.001 |
|
| 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中数学 来源： 题型：
若数列{an}满足an＋1＝an＋an＋2(n∈N*)，则称数列{an}为“凸数列”．
(1) 设数列{an}为“凸数列”，若a1＝1，a2＝－2，试写出该数列的前6项，并求出前6项之和；
(2) 在“凸数列”{an}中，求证：an＋3＝－an，n∈N*；
(3) 设a1＝a，a2＝b，若数列{an}为“凸数列”，求数列前2011项和S2 011.
查看答案和解析>>
科目：高中数学 来源： 题型：
定义在(－∞，0)∪(0，＋∞)上的函数f(x)，如果对于任意给定的等比数列{an}，{f(an)}仍是等比数列，则称f(x)为“保等比数列函数”．现有定义在(－∞，0)∪(0，＋∞)上的如下函数：
①f(x)＝x2；②f(x)＝2x；③f(x)＝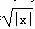
；④f(x)＝ln(x)．
其中是“保等比数列函数”的是__________．(填序号)
查看答案和解析>>
科目：高中数学 来源： 题型：
已知等差数列{an}满足：an＋1>an(n∈N*)，a1＝1，该数列的前三项分别加上1，1，3后顺次成为等比数列{bn}的前三项．
(1) 分别求数列{an}、{bn}的通项公式；
(2) 设Tn＝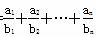
(n∈N*)，若Tn＋
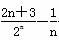<c(c∈Z)恒成立，求c的最小值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
，若
，则
的值为 （ ）
D．
