
盒中装有形状,大小完全相同的5个球,其中红色球3个,黄色球2个,若从中随机取出2个球,已知其中一个为红色,则另一个为黄色的概率为
A.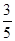 B.
B.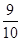 C.
C.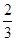 D.
D.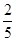
C
【解析】
试题分析:根据题意得:含有红色球的基本事件有9个,其中一红球、一黄球的基本事件有6个,由此结合古典概型的概率公式即可算出所求的概率.
解:记红色球分别为a、b、c,黄色球分别为d、e,
∵随机取出2个球,其中一个为红色,∴所有的基本事件为
(a,b),(a,c),(b,c),(a,d),(a,e),(b,d),(b,e),(c,d),(c,e)共9个
符合题意的基本事件为:(a,d),(a,e),(b,d),(b,e),(c,d),(c,e)共6个
因此,另一个为黄色的概率为:P=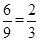 ,故选:C
,故选:C
考点:古典概型
点评:本题给出摸球事件,求在其中一个为红色的情况下,另一个为黄色的概率.着重考查了等可能事件的概率及其求法等知识,属于基础题.


科目:高中数学 来源: 题型:
| 25 | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
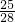 ”请你回答有几张“世博会会徽”卡呢?
”请你回答有几张“世博会会徽”卡呢?查看答案和解析>>
科目:高中数学 来源:2011年江西省新余市高考数学一模试卷(理科)(解析版) 题型:解答题
 ”请你回答有几张“世博会会徽”卡呢?
”请你回答有几张“世博会会徽”卡呢?查看答案和解析>>
科目:高中数学 来源:2010年河南省郑州市高考数学二模试卷(理科)(解析版) 题型:解答题
 ”请你回答有几张“世博会会徽”卡呢?
”请你回答有几张“世博会会徽”卡呢?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com