练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在中， ⑴ 已知： acosB=bcosA ,试判断形状;

    ⑵求证：。

    ⑴为等腰三角形⑵证明略


    解析:

    (1)由正弦定理,得 a=2RsinA,b=2RsinB ，即 acosB =bcosA。

    ∴sinA cosB=sinB cosA，即 sinA cosB- cosA sinB=0， sin(A-B)=0。

     ∴    A-B=0  ,A=B，∴为等腰三角形.

    (2) 证明：左边==-2（）。

    由正弦定理，得，故成立。已知： ==  ,试判断形状。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在等差数列{an}中，公差d≠0，a2是a1与a4的等比中项，已知数列a1，a3，ak1，ak2，…，akn，…成等比数列，求数列{kn}的通项kn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

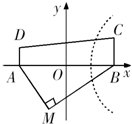    如图，某农场在M处有一堆肥料沿道路MA或MB送到大田ABCD中去，已知|MA|=6，|MB|=8，且|AD|≤|BC|，∠AMB=90°，能否在大田中确定一条界线，使位于界线一侧沿MB送肥料较近？若能，请建立适当坐标系求出这条界线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，若已知a=18，b=22，A=35°，求B时，解的个数是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    四棱锥S-ABCD中，底面ABCD为平行四边形，SO⊥底面ABCD，O在CB上．已知∠ABC=45°，AB=2，BC=2
    		2
    ，SA=SB=
    		3
    ，
    （Ⅰ）求证：平面SCB⊥平面ABCD；
    （Ⅱ）求四棱锥S-ABCD的体积；
    （Ⅲ）求直线SD与平面SAB所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源：2012年苏教版高中数学必修5 1.3正弦定理、余弦定理应用练习卷（解析版） 题型：解答题

    在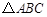中，若已知三边为连续正整数，最大角为钝角，

    （1）求最大角；

    （2）求以此最大角为内角，夹此角两边之和为4的平行四边形的最大面积．

     

    查看答案和解析>>

    同步练习册答案