Question

（09年潍坊一模文）(14分)

    设函数表示f(x)导函数。

    (I)求函数一份（x）)的单调递增区间；

    (Ⅱ)当k为偶数时，数列{}满足．证明：数列{}中

不存在成等差数列的三项；

  (Ⅲ)当后为奇数时，证明：对任意正整数，n都有成立．

Answer 1

 解析：（Ⅰ）函数的定义域为（0，+∞）

     又                      …………1分

当k为奇数时，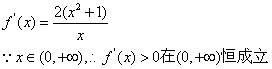

即的单调递增区间为                     …………2分

当k为偶函数时，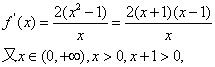

由>0，得x-1>0,∴x>1,即f(x)的单调递增区间为，…………3分

综上所述：当k为奇数时，f(x)的单调递增区间为，当k为偶数时f(x)的单调递增区间为                     4分

（Ⅱ）当k为偶数时，由（Ⅰ）知

     所以

根据题设条件有

∴{ }是以2为公式的比例数列                  …………6分

假设数列{}中存在三项，，，成等差数列

不妨设r<s<t，则2=+

即

又 ………9分

（Ⅲ）当k为奇数时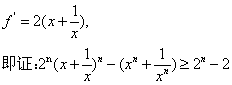        ………10分

方法二：（数学归纳发）

当n=1是，左边=0，右边=0，显然不等式成立

设n=k+1时：

又

n=k+1时结论成立。

综上，对一切正整数n结论成立。