已知f(x)的定义域为(0,+∞),且满足f(4)=1,对任意x1,x2(0,+∞),都有f(x1•x2)=f(x1)+f(x2),当x∈(0,1)时,f(x)<0.
(1)求f(1);
(2)证明f(x)在(0,+∞)上是增函数;
(3)解不等式f(3x+1)+f(2x-6)≤3.
解:(1)∵对任意x
1,x
2(0,+∞),都有f(x
1•x
2)=f(x
1)+f(x
2),
令x
1=x
2=1,
f(1•1)=f(1)+f(1),
则f(1)=0(2分)
(2)设x
1,x
2∈(0,+∞)且x
1<x
2,
∵对任意x
1,x
2(0,+∞),都有f(x
1•x
2)=f(x
1)+f(x
2),
∴则f(x
1)-f(x
2)=f(

)
∵0<x
1<x
2,
∴0<

<1,又当x∈(0,1)时,f(x)<0,∴f(x
1)-f(x
2)=
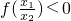
,
∴f(x)在(0,+∞)上是增函数(7分)
(3)令x
1=x
2=4,则f(16)=f(4)+f(4)=2,
令x
1=4,x
2=16,则f(64)=f(4)+f(16)=3(9分)
∴f(3x+1)+f(2x-6)≤3=f(64)
∴
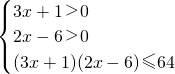
∴x∈(3,5](12分)
分析:(1)由已知中f(x
1•x
2)=f(x
1)+f(x
2),令x
1=x
2=1,可得f(1)的值;
(2)由f(x
1•x
2)=f(x
1)+f(x
2),可得f(x
1)-f(x
2)=f(

),结合x∈(0,1)时,f(x)<0.及增函数的定义可证得结论
(3)令x1=x2=4,可得f(16)=2,x1=4,x2=16,可得f(64)=3,结合f(x)的定义域为(0,+∞),f(x
1•x
2)=f(x
1)+f(x
2),及(2)中函数的单调性,可将不等式f(3x+1)+f(2x-6)≤3转化为一个关于x的不等式组.本题考查的知识点是抽象函数及其应用
点评:本题考查的是函数的单调性证明问题.抽象函数的奇偶性的判定,以及赋值法的应用,属于中档题,在解答的过程当中充分体现了函数单调性的定义、作差法以及赋值法等知识.值得同学们体会和反思.

 )
) <1,又当x∈(0,1)时,f(x)<0,∴f(x1)-f(x2)=
<1,又当x∈(0,1)时,f(x)<0,∴f(x1)-f(x2)=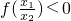 ,
,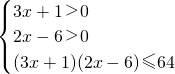 ∴x∈(3,5](12分)
∴x∈(3,5](12分) ),结合x∈(0,1)时,f(x)<0.及增函数的定义可证得结论
),结合x∈(0,1)时,f(x)<0.及增函数的定义可证得结论
