
已知函数 ,其中
,其中 ,记函数
,记函数 的定义域为D.
的定义域为D.
(1)求函数 的定义域D;
的定义域D;
(2)若函数 的最小值为
的最小值为 ,求
,求 的值;
的值;
(3)若对于D内的任意实数 ,不等式
,不等式 <
< 恒成立,求实数
恒成立,求实数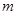 的取值范围.
的取值范围.
(1)
(2) 
(3) (-∞, )∪[
)∪[ ,+∞)
,+∞)
【解析】
试题分析:解:(1)要使函数有意义:则有 ,解得
,解得
∴ 函数的定义域D为 2分
2分
(2)


 ,
, ,即
,即 , 5分
, 5分
由 ,得
,得 ,
, .
7分
.
7分
(注: 不化简为
不化简为 扣1分)
扣1分)
(3)由题知-x2+2mx-m2+2m<1在x∈ 上恒成立,
上恒成立,
 -2mx+m2-2m+1>0在x∈
-2mx+m2-2m+1>0在x∈ 上恒成立, 8分
上恒成立, 8分
令g(x)=x2-2mx+m2-2m+1,x∈ ,
,
配方得g(x)=(x-m)2-2m+1,其对称轴为x=m,
当m≤-3时, g(x)在 为增函数,
为增函数,
∴g(-3)= (-3-m)2-2m+1= m2+4m +10≥0,
而m2+4m +10≥0对任意实数m恒成立,∴m≤-3. 10分
②当-3<m<1时,函数g(x)在(-3,-1)为减函数,在(-1, 1)为增函数,
∴g(m)=-2m+1>0,解得m< ∴-3<m<
∴-3<m< 12分
12分
③当m≥1时,函数g(x)在 为减函数,∴g(1)= (1-m)2-2m+1= m2-4m +2≥0,
为减函数,∴g(1)= (1-m)2-2m+1= m2-4m +2≥0,
解得m≥ 或m≤
或m≤ , ∴-3<m<
, ∴-3<m< 14分
14分
综上可得,实数m的取值范围是 (-∞, )∪[
)∪[ ,+∞) 16分
,+∞) 16分
考点:函数的概念和值域,二次函数的最值
点评:解决的关键是利用函数的概念以及分离参数的思想来借助于二次函数的最值得到参数的范围。属于基础题。


科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | an |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年大连市双基测试文)(14分)已知等差数列{an}满足![]() ,设Sn是数列
,设Sn是数列![]() 的前n项和,
的前n项和,
记![]()
(1)求![]() ;
;
(2) 比较![]() 与
与![]() 其中
其中![]() 的大小;
的大小;
(3)如果函数![]() 对一切大于1的正整数n其函数值都小于零,那么a、b应满足什么条件.
对一切大于1的正整数n其函数值都小于零,那么a、b应满足什么条件.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2010年上海市金山区高考数学一模试卷(文理合卷)(解析版) 题型:解答题
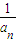 }的前n项和,记f(n)=S2n-Sn,
}的前n项和,记f(n)=S2n-Sn,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com