
如图所示,已知AD、BE是△ABC的高,![]() 、
、![]() 是△
是△![]() 的高,且AB∶AD=
的高,且AB∶AD=![]() ∶
∶![]() ,∠C=∠
,∠C=∠![]() .
.
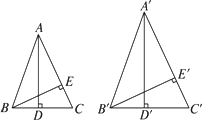
求证:AD·![]() =
=![]() ·BE.
·BE.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:044
一架飞机以
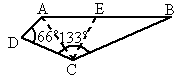
360km/h的速度,沿北偏东75°的航向从城市A出发向城市B飞行,18min以后,飞机由于天气原因按命令改飞另一个城市C,如图所示,已知AD=57km,CD=110km,BC=204km,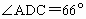 ,
,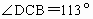 ,问收到命令时飞机应该沿什么航向飞行,此时离城市C的距离是多少?
,问收到命令时飞机应该沿什么航向飞行,此时离城市C的距离是多少?
查看答案和解析>>
科目:高中数学 来源:教材完全解读 高中数学 必修5(人教B版课标版) 人教B版课标版 题型:044
一架飞机以360 km/h的速度,沿北偏东75°的航向从城市A出发向城市B飞行,18 min以后,飞机由于天气原因按命令改飞另一个城市C.如图所示,已知AD=57 km,CD=110 km,BC=204 km,∠ADC=66°,∠DCB=133°,问收到命令时,飞机应该沿什么航向飞行,此时离城市C的距离是多少?

查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
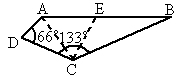
一架飞机以360km/h的速度,沿北偏东75°的航向从城市A出发向城市B飞行,18min以后,飞机由于天气原因按命令改飞另一个城市C,如图所示,已知AD=57km,CD=110km,BC=204km,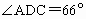 ,
,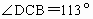 ,问收到命令时飞机应该沿什么航向飞行,此时离城市C的距离是多少?
,问收到命令时飞机应该沿什么航向飞行,此时离城市C的距离是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com