
函数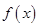 的定义域为
的定义域为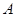 ,若
,若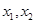
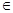
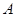 ,且
,且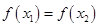 时总有
时总有 ,则称
,则称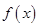 为单函数.例如
为单函数.例如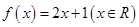 是单函数,现给出下列结论:
是单函数,现给出下列结论:
①函数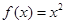
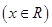 是单函数;
是单函数;
②函数 是单函数;
是单函数;
③偶函数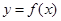 ,
,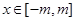 (
(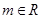 )有可能是单函数;
)有可能是单函数;
④在定义域上具有单调性的函数一定是单函数.
其中的正确的结论是 (写出所有正确结论的序号).
②④
【解析】
试题分析:因为根据题意 为单函数,说明一个x对应一个y,反之呢,一个y对应一个x,因此根据对于概念的理解, 得到
为单函数,说明一个x对应一个y,反之呢,一个y对应一个x,因此根据对于概念的理解, 得到
命题1中,函数是二次函数,显然不满足一个y对应一个x。舍去
命题2中,是指数函数,在整个定义域内严格递增,那么满足单函数的定义,成立。
命题3中,由于函数是抽象函数,且为偶函数 ,
,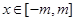 (
(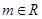 )有可能是单函数,不能满足。因为f(-m)=f(m),不同的变量也有同一个函数值。故错误
)有可能是单函数,不能满足。因为f(-m)=f(m),不同的变量也有同一个函数值。故错误
命题4中,在定义域上具有单调性的函数一定是单函数.
显然符合定义,故成立,正确的命题序号为②④
考点:本试题考查了新定义的运用。
点评:理解这里的单函数实际上就是一一对应的函数,那么利用这一点逐项分析,结合指数函数和幂函数的性质来得到结论。属于中档题。


 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
设函数![]() 的定义域为
的定义域为![]() ,若存在常数
,若存在常数![]() ,使
,使![]() 对一切实数
对一切实数![]() 均成立,则称
均成立,则称![]() 为
为![]() 函数.给出下列函数:
函数.给出下列函数:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 是定义在
是定义在![]() 上的奇函数,且满足对一切实数
上的奇函数,且满足对一切实数![]() 、
、![]() 均有
均有![]() .其中是
.其中是![]() 函数的序号为 。
函数的序号为 。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南省邓州一高分校高三上学期第四次周考文科数学试卷(解析版) 题型:解答题
设命题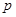 :函数
:函数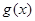 =
= 是
是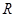 上的减函数,命题
上的减函数,命题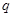 :函数
:函数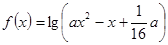 的定义域为
的定义域为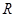 ,若“
,若“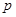 且
且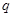 ”为假命题,“
”为假命题,“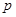 或
或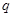 ”为真命题,求实数
”为真命题,求实数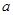 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省温州市高三上学期期初考试理科数学试卷(解析版) 题型:填空题
设函数 的定义域为
的定义域为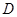 ,若存在非零实数
,若存在非零实数 使得对于任意
使得对于任意 ,有
,有 ,且
,且 ,则称
,则称 为
为 上的
上的 高调函数.如果定义域是
高调函数.如果定义域是 的函数
的函数 为
为 上的
上的 高调函数,那么实数
高调函数,那么实数 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省高三第一次月考文科数学试卷(解析版) 题型:填空题
设函数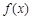 的定义域为
的定义域为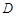 ,若存在非零实数
,若存在非零实数 使得对于任意
使得对于任意 ,有
,有 ,且
,且 ,则称
,则称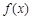 为
为 上的“高调函数”.现给出下列命题:
上的“高调函数”.现给出下列命题:
①函数 为
为 上的“1高调函数”;
上的“1高调函数”;
②函数 为
为 上的“
上的“ 高调函数”;
高调函数”;
③如果定义域为 的函数
的函数 为
为 上“
上“ 高调函数”,那么实数
高调函数”,那么实数 的取值范围是
的取值范围是 ;
;
其中正确的命题是 .(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源:2013届江苏省无锡市高二下期中数学试卷(成志班)(解析版) 题型:填空题
设函数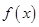 的定义域为
的定义域为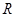 ,若存在常数
,若存在常数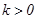 ,使
,使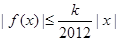 对一切实数
对一切实数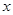 均成立,则称
均成立,则称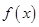 为“海宝”函数. 给出下列函数:
为“海宝”函数. 给出下列函数:
①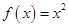 ;②
;② ;③
;③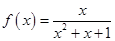 ;④
;④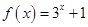
其中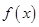 是“海宝”函数的序号为
是“海宝”函数的序号为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com