
| 类 型 | A规格 | B规格 | C规格 |
| 第一种钢板 | 1 | 2 | 1 |
| 第二种钢板 | 1 | 1 | 3 |
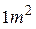 ,第二种为
,第二种为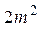 ,今需要A、B、C三种规格的成品各12、15、27块,问各截这两种钢板多少张,可得所需三种规格成品,且使所用钢板面积最小?
,今需要A、B、C三种规格的成品各12、15、27块,问各截这两种钢板多少张,可得所需三种规格成品,且使所用钢板面积最小?科目:高中数学 来源:不详 题型:单选题
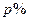 ,第二次提价
,第二次提价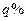 ;
;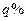 ,第二次提价
,第二次提价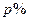 ;
;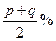 ,第二次提价
,第二次提价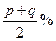 ,
,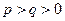 ,比较上述三种方案,提价最多的是
,比较上述三种方案,提价最多的是| A.甲 | B.乙 | C.丙 | D.一样多 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com