
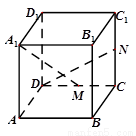
如图,在正方体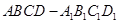 中,
中,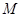 、
、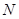 分别是
分别是 、
、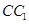 的中点,则异面直线
的中点,则异面直线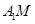 与
与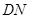 所成的角的大小是____________。
所成的角的大小是____________。
90º
【解析】方法一:连接D1M,易得DN⊥A1D1 ,DN⊥D1M,
所以,DN⊥平面A1MD1,
又A1M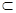 平面A1MD1,所以,DN⊥A1D1,故夹角为90º[来源:Zxxk.Com]
平面A1MD1,所以,DN⊥A1D1,故夹角为90º[来源:Zxxk.Com]
方法二:以D为原点,分别以DA, DC, DD1为x, y, z轴,建立空间直角坐标系D—xyz.设正方体边长为2,则D(0,0,0),N(0,2,1),M(0,1,0)A1(2,0,2)
故,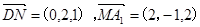
所以,cos<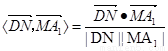 = 0,故DN⊥D1M,所以夹角为90º[来源:Z#xx#k.Com]
= 0,故DN⊥D1M,所以夹角为90º[来源:Z#xx#k.Com]
[点评]异面直线夹角问题通常可以采用两种途径: 第一,把两条异面直线平移到同一平面中借助三角形处理; 第二,建立空间直角坐标系,利用向量夹角公式解决.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
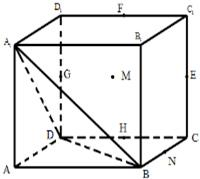 如图,在正方体中,边长为a,EFGH分别是的CC1、C1D1、D1D、DC的中点,N是BC的中点,M在四边形GHEF上及其内部运动,若MH∥平面A1BD,则点M轨迹的长度是( )
如图,在正方体中,边长为a,EFGH分别是的CC1、C1D1、D1D、DC的中点,N是BC的中点,M在四边形GHEF上及其内部运动,若MH∥平面A1BD,则点M轨迹的长度是( )| A、a | ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在正方体中,O是下底面的中心,B′H⊥D′O,H为垂足,求证:
如图,在正方体中,O是下底面的中心,B′H⊥D′O,H为垂足,求证:查看答案和解析>>
科目:高中数学 来源:2014届浙江省高二10月月考文科数学试卷(解析版) 题型:解答题
如图,在正方体 中,
中, 为底面
为底面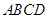 的中心,
的中心, 是
是 的中点,设
的中点,设 是
是 上的中点,求证:(1)
上的中点,求证:(1) ;
;
(2)平面 ∥平面
∥平面 .
.

查看答案和解析>>
科目:高中数学 来源:河北省2009-2010学年度第二学期二调考试高一年级数学试卷理科 题型:选择题
如图,在正方体 中,E、F、G、H分别为中点,则异面直线EF与GH所成的角等于( )
中,E、F、G、H分别为中点,则异面直线EF与GH所成的角等于( )
 A.
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com