
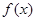 对任意
对任意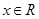 都有
都有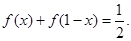
(Ⅰ)求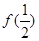 和
和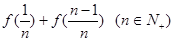 的值.
的值.
(Ⅱ)数列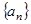 满足:
满足: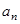 =
=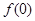 +
+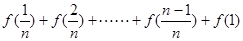 ,数列
,数列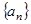 是等差数列吗?请给予证明;
是等差数列吗?请给予证明;
(Ⅲ)令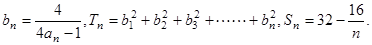 试比较
试比较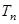 与
与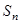 的大小.
的大小.
(Ⅰ)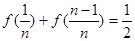 .(Ⅱ)
.(Ⅱ)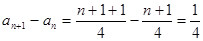 .
.
(Ⅲ)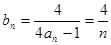 ,利用“放缩法”。
,利用“放缩法”。
【解析】
试题分析:(Ⅰ)因为 .所以
.所以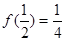 . 2分
. 2分
令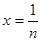 ,得
,得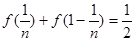 ,即
,即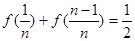 .
4分
.
4分
(Ⅱ)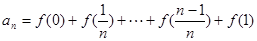
又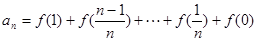 5分
5分
两式相加
 .
.
所以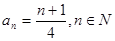 , 7分
, 7分
又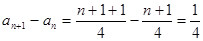 .故数列
.故数列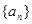 是等差数列.
9分
是等差数列.
9分
(Ⅲ)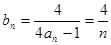
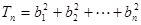
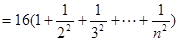
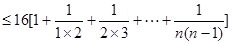 10分
10分
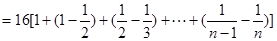 12分
12分
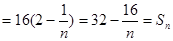
所以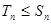 14分
14分
考点:本题主要考查抽象函数问题,等差数列的证明,“放缩法”证明不等式,“裂项相消法”。
点评:中档题,本题具有较强的综合性,本解答从确定数列相邻项的关系入手,认识到数列的特征,利用“错位相消法”达到求和目的。“分组求和法”“裂项相消法”“错位相减法”是高考常常考到数列求和方法。(III)先将和式通过放缩利用“裂项相消法”实现求和,达到证明目的。


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
(本小题满分13分)已知向量a = ![]() ,b =
,b =![]() , 且存在实数
, 且存在实数![]() ,使向量m = a
,使向量m = a![]() b, n =
b, n = ![]() a
a![]() b, 且m⊥n. (Ⅰ)求函数
b, 且m⊥n. (Ⅰ)求函数![]() 的关系式,并求其单调区间和极值; (Ⅱ)是否存在正数M,使得对任意
的关系式,并求其单调区间和极值; (Ⅱ)是否存在正数M,使得对任意![]() ,都有
,都有![]() 成立?若存在求出M;若不存在,说明理由.
成立?若存在求出M;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:山东省明天中学2010届高三上学期期中考试 题型:解答题
已知向量a =  ,b
=
,b
=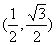 ,且存在实数
,且存在实数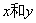 ,使向量m = a
,使向量m = a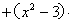 b,
n =
b,
n =  a
a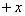 b,且m⊥n.
b,且m⊥n.
(Ⅰ)求函数 的关系式,并求其单调区间和极值;
的关系式,并求其单调区间和极值;
(Ⅱ)是否存在正数M,使得对任意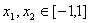 ,都有
,都有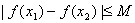 成立?若存在求出M;若不存在,说明理由.
成立?若存在求出M;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com