
设 是定义在
是定义在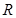 上的可导函数,则
上的可导函数,则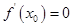 是
是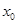 为函数
为函数 的极值点的( )
的极值点的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
科目:高中数学 来源:2010-2011年辽宁省高二下学期期末考试数学理科 题型:解答题
(本小题满分12分)(1)对于定义在 上的函数
上的函数 ,满足
,满足 ,求证:函数
,求证:函数 在
在 上是减函数;
上是减函数;
(2)请你认真研读(1)中命题并联系以下命题:若 是定义在
是定义在 上的可导函数,满足
上的可导函数,满足 ,则
,则 是
是 上的减函数。然后填空建立一个普遍化的命题
上的减函数。然后填空建立一个普遍化的命题 :
:
设 是定义在
是定义在 上的可导函数,
上的可导函数, ,若
,若  +
+
 ,
,
则 是 上的减函数。
上的减函数。
注:命题的普遍化就是从考虑一个对象过渡到考虑包含该对象的一个集合;或者从考虑一个较小的集合过渡到考虑包含该较小集合的更大集合。
(3)证明(2)中建立的普遍化命题。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省资阳市二下学期期末质量检测文科数学试卷(解析版) 题型:选择题
设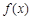 是定义在
是定义在 上的可导函数,且满足
上的可导函数,且满足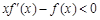 . 若
. 若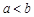 且
且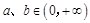 ,则
,则
(A) (B)
(B)
(C)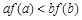 (D)
(D)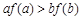
查看答案和解析>>
科目:高中数学 来源:2010-2011年河南省许昌市高二下学期联考数学理卷 题型:选择题
设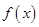 是定义在
是定义在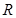 上的可导函数,则
上的可导函数,则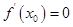 是
是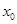 为函数
为函数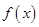 的极值点的( )
的极值点的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2010-2011年河南省卫辉市高二4月月考数学理卷 题型:选择题
设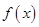 是定义在
是定义在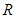 上的可导函数,则
上的可导函数,则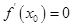 是
是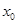 为函数
为函数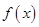 的极值点的( )
的极值点的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com