
已知点 和圆
和圆 :
: .
.

(Ⅰ)过点 的直线
的直线 被圆
被圆 所截得的弦长为
所截得的弦长为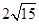 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)若 的面积
的面积 ,且
,且 是圆
是圆 内部第一、二象限的整点(平面内横、纵坐标均为整数
内部第一、二象限的整点(平面内横、纵坐标均为整数
的点称为整点),求出点 的坐标.
的坐标.
(Ⅰ)方程为: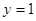 或
或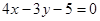 ;(Ⅱ)
;(Ⅱ)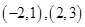 .
.
【解析】
试题分析:(Ⅰ)当所求直线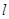 的斜率不存在时,弦长为
的斜率不存在时,弦长为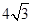 ,不符合要求.因此可设直线
,不符合要求.因此可设直线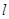 的斜率为
的斜率为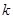 ,根据点斜式写出直线方程
,根据点斜式写出直线方程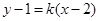 ,求出圆心到直线的距离
,求出圆心到直线的距离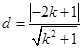 ,再由勾股定理得到:
,再由勾股定理得到: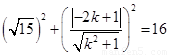 ,解得
,解得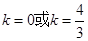 ;(Ⅱ)连结
;(Ⅱ)连结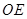 ,求出圆与
,求出圆与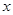 轴的两个交点
轴的两个交点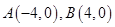 .并连结
.并连结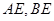 ,得到
,得到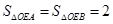 ,因此要使
,因此要使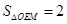 ,那么点
,那么点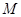 必在经过点
必在经过点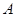 且与直线
且与直线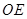 平行的直线上.结合点
平行的直线上.结合点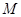 所在象限,可以求出
所在象限,可以求出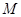 为
为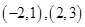 .
.
试题解析:(Ⅰ)当所求直线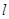 的斜率不存在时,弦长为
的斜率不存在时,弦长为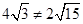 ,不符合要求;
,不符合要求;
因此设直线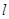 的斜率为
的斜率为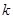 ,那么直线
,那么直线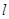 的方程为:
的方程为: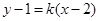 .
.
所以圆心到直线的距离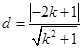 ,又因为半径
,又因为半径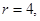 弦长为
弦长为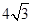 .
.
所以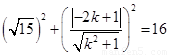 ,解得:
,解得: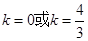 .
.
所以所求直线方程为: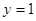 或
或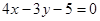 ;
;
(Ⅱ)连结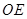 ,点
,点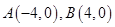 满足
满足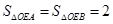 ,
,
过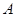 作直线
作直线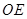 的平行线
的平行线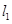 .
.
∵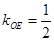
∴直线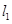 的方程分别为:
的方程分别为:
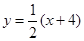
设点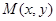 (
(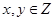 且
且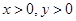 )
)
∴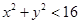
解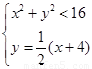 ,得:
,得: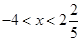
∵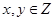 且
且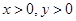 ,在
,在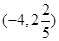 上
上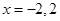 对应的
对应的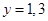 .
.
∴满足条件的点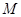 存在,共有2个,它们的坐标分别为:
存在,共有2个,它们的坐标分别为: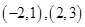 .
.
考点:直线与圆的位置关系,点与圆的位置关系,直线方程.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源:2013-2014学年安徽省“皖西七校”高三年级联合考试理科数学试卷(解析版) 题型:解答题
在平面直角坐标系中,已知点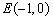 和
和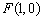 ,圆
,圆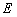 是以
是以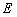 为圆心,半径为
为圆心,半径为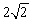 的圆,点
的圆,点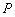 是圆
是圆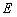 上任意一点,线段
上任意一点,线段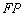 的垂直平分线
的垂直平分线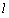 和半径
和半径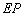 所在的直线交于点
所在的直线交于点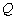 .
.
(Ⅰ)当点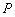 在圆上运动时,求点
在圆上运动时,求点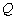 的轨迹方程
的轨迹方程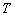 ;
;
(Ⅱ)已知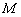 ,
,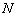 是曲线
是曲线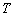 上的两点,若曲线
上的两点,若曲线 上存在点
上存在点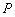 ,满足
,满足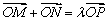 (
( 为坐标原点),求实数
为坐标原点),求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届浙江绍兴一中高二第一学期期中测试理科数学试卷(解析版) 题型:解答题
已知点 和圆
和圆 :
: .
.

(Ⅰ)过点 的直线
的直线 被圆
被圆 所截得的弦长为
所截得的弦长为 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)试探究是否存在这样的点 :
: 是圆
是圆 内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEM的面积
内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEM的面积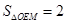 ?若存在,求出点
?若存在,求出点 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省嘉兴市高三第二次模拟考试理科数学试卷(解析版) 题型:填空题
已知点 和圆
和圆 :
: ,
, 是圆
是圆 的直径,
的直径, 和
和 是
是 的三等分点,
的三等分点, (异于
(异于 )是圆
)是圆 上的动点,
上的动点, 于
于 ,
, ,直线
,直线 与
与 交于
交于 ,则当
,则当 时,
时, 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年黑龙江省哈尔滨市高三第四次模拟考试理科数学试卷(解析版) 题型:解答题
已知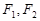 分别为椭圆
分别为椭圆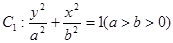 的上下焦点,其中
的上下焦点,其中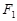 也是抛物线
也是抛物线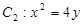 的焦点,点
的焦点,点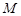 是
是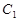 与
与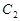 在第二象限的交点,且
在第二象限的交点,且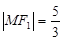 .
.
(1)
求椭圆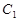 的方程;(5分)
的方程;(5分)
(2)
已知点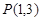 和圆
和圆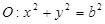 ,过点
,过点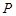 的动直线
的动直线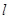 与圆
与圆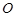 相交于不同的两
相交于不同的两
点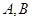 ,在线段
,在线段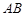 上取一点
上取一点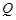 ,满足
,满足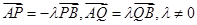 且
且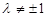 .
.
求证:点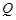 总在某定直线上.(7分)
总在某定直线上.(7分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com