
已知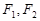 分别为椭圆
分别为椭圆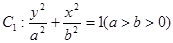 的上下焦点,其中
的上下焦点,其中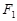 也是抛物线
也是抛物线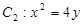 的焦点,点
的焦点,点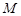 是
是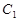 与
与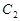 在第二象限的交点,且
在第二象限的交点,且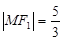 .
.
(1)
求椭圆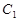 的方程;(5分)
的方程;(5分)
(2)
已知点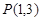 和圆
和圆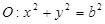 ,过点
,过点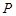 的动直线
的动直线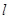 与圆
与圆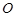 相交于不同的两
相交于不同的两
点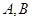 ,在线段
,在线段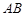 上取一点
上取一点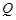 ,满足
,满足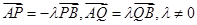 且
且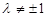 .
.
求证:点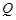 总在某定直线上.(7分)
总在某定直线上.(7分)
(1)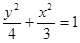 (2)见解析
(2)见解析
【解析】(I)根据抛物线的焦点坐标可求出c值,然后利用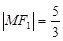 和抛物线的焦半径公式求出点M的坐标,根据点M在椭圆上,建立方程可求出椭圆的标准方程.
和抛物线的焦半径公式求出点M的坐标,根据点M在椭圆上,建立方程可求出椭圆的标准方程.
(1)
证明点Q总在一条直线上,就是证明点Q的坐标总是满足某条直线方程,设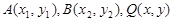 ,由
,由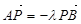 和
和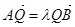 可得四个方程,然后再结合点A、B都在圆上,对四个方程进行变形求解
可得四个方程,然后再结合点A、B都在圆上,对四个方程进行变形求解
(1)由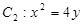 知,
知,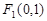 ,设
,设 ,因
,因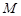 在抛物线
在抛物线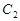 上,故
上,故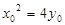 ,又
,又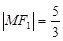 ,则
,则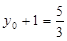 ,得
,得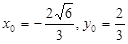 ,而点
,而点
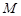 在椭圆上,有
在椭圆上,有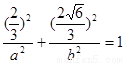 ,又
,又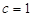 ,所以椭圆方程为
,所以椭圆方程为
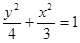 (5分)
(5分)
(2)设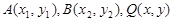 ,由
,由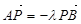 ,得
,得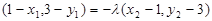 ,即
,即 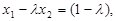 ①
① 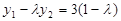 ②
②
由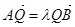 ,得
,得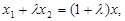 ③
③ 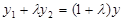 ,
④ -------- (7分)
,
④ -------- (7分)
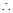 ①
①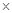 ③,得
③,得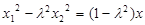 , ②
, ②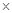 ④,得
④,得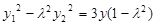 -----(9分)
-----(9分)
两式相加得  ,又点
,又点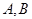 在圆
在圆
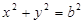 上,由(1)知,即在圆
上,由(1)知,即在圆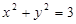 上,且
上,且 ,
,
(2)
 ,即
,即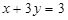 ,
,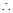 点
点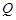 总在定直线
总在定直线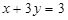 上
上


科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知抛物线y2=8x与椭圆
已知抛物线y2=8x与椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•德州一模)已知F1,F2分别为椭圆C1:
(2013•德州一模)已知F1,F2分别为椭圆C1:| x2 |
| b2 |
| y2 |
| a2 |
| 3 |
| 5 |
| OA |
| OB |
| OP |
查看答案和解析>>
科目:高中数学 来源:黑龙江省哈尔滨市第六中学2012届高三第四次模拟考试数学理科试题 题型:044
已知F1,F2分别为椭圆![]() 的上下焦点,其中F1也是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=
的上下焦点,其中F1也是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=![]() .
.
(1)求椭圆C1的方程;
(2)已知点P(1,3)和圆O:x2+y2=b2,过点P的动直线l与圆O相交于不同的两点A,B,在线段AB上取一点Q,满足![]() 且λ≠±1.
且λ≠±1.
求证:点Q总在某定直线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com