
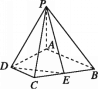
【题目】如图,在四棱锥P﹣ABCD中,PC⊥平面PAD,AB∥CD,CD=2AB=2BC,M,N分别是棱PA,CD的中点. 
(1)求证:PC∥平面BMN;
(2)求证:平面BMN⊥平面PAC. 
【答案】
(1)证明:设AC∩BN=O,连结MO,AN,
因为 ![]() ,N为CD的中点,
,N为CD的中点,
所以AB=CN,AB∥CN,所以四边形ABCN为平行四边形,
所以O为AC的中点,所以MO∥PC.
又因为MO平面BMN,PC平面BMN,所以PC∥平面BMN
(2)证明:(方法一)因为PC⊥平面PDA,AD平面PDA
所以PC⊥AD,由(1)同理可得,四边形ABND为平行四边形,
所以AD∥BN,所以BN⊥PC
因为BC=AB,所以平行四边形ABCN为菱形,所以BN⊥AC,
因为PC∩AC=C,AC平面PAC,PC平面PAC,所以BN⊥平面PAC
因为BN平面BMN,所以平面BMN⊥平面PAC.
(方法二)连结PN,因为PC⊥平面PDA,PA平面PDA,所以PC⊥PA
因为PC∥MO,所以PA⊥MO,因为PC⊥平面PDA,PD平面PDA,所以PC⊥PD
因为N为CD的中点,所以 ![]() ,由(1)
,由(1) ![]() ,所以AN=PN
,所以AN=PN
又因为M为PA的中点,所以PA⊥MN
因为MN∩MO=M,MN平面BMN,MO平面BMN
所以PA⊥平面BMN,因为PA平面PAC,所以平面PAC⊥平面BMN.
【解析】
【考点精析】掌握直线与平面平行的判定和平面与平面垂直的判定是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A.x∈R,2x>x2
B.若a>b,c>d,则 a﹣c>b﹣d
C.x∈R,ex<0
D.ac2<bc2是a<b的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是 ( )
A. “x<1”是“log2(x+1)<1”的充分不必要条件
B. 命题“x>0,2x>1”的否定是“x0≤0,![]() ≤1”
≤1”
C. 命题“若a≤b,则ac2≤bc2”的逆命题是真命题
D. 命题“若a+b≠5,则a≠2或b≠3”的逆否命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,∠BAD=∠ADC=90°,E为CB的中点,AB=PA=AD=2CD,则AP与平面PDE所成角的正弦值为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆过定点P(4,0),且在y轴上截得的弦MN的长为8.
(1)求动圆圆心C的轨迹方程;
(2)过点(2,0)的直线l与动圆圆心C的轨迹交于A,B两点,求证:![]() 是一个定值.
是一个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知M,N是焦点为F的抛物线y2=2px(p>0)上两个不同的点,线段MN的中点A的横坐标为![]() .
.
(1)求|MF|+|NF|的值;
(2)若p=2,直线MN与x轴交于点B,求点B的横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙两人进行围棋比赛,共比赛2n(n∈N+)局,根据以往比赛胜负的情况知道,每局甲胜的概率和乙胜的概率均为 ![]() .如果某人获胜的局数多于另一人,则此人赢得比赛.记甲赢得比赛的概率为P(n).
.如果某人获胜的局数多于另一人,则此人赢得比赛.记甲赢得比赛的概率为P(n).
(1)求P(2)与P(3)的值;
(2)试比较P(n)与P(n+1)的大小,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn}均为各项都不相等的数列,Sn为{an}的前n项和,an+1bn=Sn+1(n∈N).
(1)若a1=1,bn= ![]() ,求a4的值;
,求a4的值;
(2)若{an}是公比为q的等比数列,求证:存在实数λ,使得{bn+λ}为等比数列;
(3)若{an}的各项都不为零,{bn}是公差为d的等差数列,求证:a2 , a3 , …,an…成等差数列的充要条件是d= ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com