
(Ⅰ)若C在点M法线的斜率为-![]() ,求点M的坐标(x0,y0);
,求点M的坐标(x0,y0);
(Ⅱ)设P(-2,a)为C对称轴上的一点,在C上是否存在点,使得C在该
点的法线通过点P?若有,求出这些点,以及C在这些点的法线方程;若没有,请说明理由.
22.本小题主要考查导数的几何意义和应用,直线方程以及综合运用数学知识解决问题的能力. 解:
(Ⅰ)函数y=x2+4x+![]() 的导数
的导数
![]() =2x+4
=2x+4
C上点(x0,y0)处切线的斜率
k0=2x0+4,
因为过点(x0,y0)的法线斜率为-![]() ,
,
所以 -![]() (2x0+4)=-1,
(2x0+4)=-1,
解得x0=-1,y0=![]() ,
,
故点M的坐标为(-1,![]() ).
).
(Ⅱ)设M(x0,y0)为C上一点.
(i)若x0=-2,则C上点M(-2,-![]() )处的切线斜率k=0,过点M(-2,-
)处的切线斜率k=0,过点M(-2,-![]() )的法线方程为x=-2,此法线过点P(-2,a).
)的法线方程为x=-2,此法线过点P(-2,a).
(ii)若x0≠-2,则过点M(x0,y0)的法线方程为
y-y0=-![]() (x-x0). ①
(x-x0). ①
若法线过P(-2,a),则a-y0=-![]() (-2-x0),
(-2-x0),
即 (x0+2)2=a. ②
若a>0,则x0=-2±![]() ,从而
,从而
y0=x![]() +4x0+
+4x0+![]() =
=![]() ,
,
将上式代入①,化简得
x+2![]() y+2-2a
y+2-2a![]() =0,
=0,
x-2![]() y+2+2a
y+2+2a![]() =0.
=0.
若a=0,则与x0≠-2矛盾.
若a<0,则②式无解.
综上,当a>0时,在C上有三个点(-2+![]() ,
,![]() ),(-2-
),(-2-![]() ,
,![]() )
)
及(-2,-![]() ).在这三点的法线过点P(-2,a),其方程分别是:
).在这三点的法线过点P(-2,a),其方程分别是:
x+2![]() y+2-2a
y+2-2a![]() =0,
=0,
x-2![]() y+2+2a
y+2+2a![]() =0,
=0,
x=-2.
当a≤0时,在C上有一个点(-2,-![]() ),在这点的法线过点P(-2,a),其方
),在这点的法线过点P(-2,a),其方
程为:
x=-2.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:湖北省襄阳五中2012届高三上学期期中考试数学文科试题 题型:044
已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切,过原点O作倾斜角为![]() 的直线n,交l于点A,交圆M于另一点B,且AO=BO=2
的直线n,交l于点A,交圆M于另一点B,且AO=BO=2
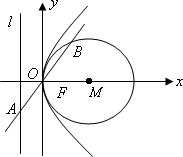
(1)求圆M和抛物线C的方程;
(2)若P为抛物线C上的动点,求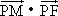 的最小值;
的最小值;
(3)过l上的动点Q向圆M作切线,切点为S,T,判断直线ST是否恒过定点?若恒过定点,求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源:浙江省东阳中学2012届高三上学期期中考试数学文科试题 题型:044
已知抛物线C:y=mx2(m>0),焦点为F,直线2x-y+2=0交抛物线C于A、B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.
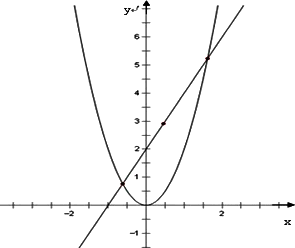
(1)若抛物线C上有一点F(xR,2)到焦点F的距离为3,求此时m的值;
(2)是否存在实数m,使△ABQ是以Q为直角顶点的直角三角形?若存在,求出m的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南省郴州市高三下学期第六次月考文科数学 题型:解答题
(本小题满分13分)
已知抛物线C:y=2x2,直线y=kx+2交C于A,B两点,M是线段AB的中点,过M作x轴
的垂线交C于点N.(1)证明:抛物线C在点N处的切线与AB平行;
(2)是否存在实数k使·=0,若存在,求k的值;若不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源:2011-2012年福建省福州市高二上学期期末考试理科数学 题型:填空题
已知抛物线C的顶点为坐标原点,焦点在x轴上,直线y=x与抛物线C交于A,B两点,若P(2,2)为AB的中点,则抛物线C的方程为________.
查看答案和解析>>
科目:高中数学 来源:2011-2012年广东省高二12月月考理科数学 题型:填空题
已知抛物线C的顶点为坐标原点,焦点在x轴上,直线y=x与抛物线C交于A,B两点,若P(2,2)为AB的中点,则抛物线C的方程为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com