
【题目】下列四个结论中:
(1)如果两个函数都是增函数,那么这两个函数的积运算所得函数为增函数;
(2)奇函数f(x)在[0,+∞)上是增函数,则f(x)在R上为增函数;
(3)既是奇函数又是偶函数的函数只有一个;
(4)若函数f(x)的最小值是a,最大值是b,则f(x)值域为[a,b].
其中正确结论的序号为 .
【答案】(2)
【解析】解:(1),当x∈(0,+∞)时,y=x与y=﹣ ![]() 均为增函数,但这两个函数的积运算所得函数为y=x(﹣
均为增函数,但这两个函数的积运算所得函数为y=x(﹣ ![]() )=﹣1不是增函数(为常函数),故(1)错误;(2)奇函数f(x)在[0,+∞)上是增函数,则f(x)在(﹣∞,0)上也是增函数,故在R上为增函数,(2)正确;(3)既是奇函数又是偶函数的函数只有一个,错误.如x∈(﹣1,1)时,f(x)=0既是奇函数又是偶函数的函数;f(x)=
)=﹣1不是增函数(为常函数),故(1)错误;(2)奇函数f(x)在[0,+∞)上是增函数,则f(x)在(﹣∞,0)上也是增函数,故在R上为增函数,(2)正确;(3)既是奇函数又是偶函数的函数只有一个,错误.如x∈(﹣1,1)时,f(x)=0既是奇函数又是偶函数的函数;f(x)= ![]() +
+ ![]() 既是奇函数又是偶函数的函数,故(3)错误;(4)若a<b,函数f(x)=
既是奇函数又是偶函数的函数,故(3)错误;(4)若a<b,函数f(x)= ![]() ,即函数f(x)的最小值是a,最大值是b,则f(x)值域为{a,b},而不是[a,b],故(4)错误.
,即函数f(x)的最小值是a,最大值是b,则f(x)值域为{a,b},而不是[a,b],故(4)错误.
所以答案是:(2).
【考点精析】本题主要考查了命题的真假判断与应用的相关知识点,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
E是PC的中点.求证:

(Ⅰ)CD⊥AE;
(Ⅱ)PD⊥平面ABE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A={x|x2﹣2x﹣8<0},B={x|x2+2x﹣3>0},C={x|x2﹣3ax+2a2<0},
(1)求A∩B.
(2)试求实数a的取值范围,使C(A∩B).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在国家“大众创业,万众创新”战略下,某企业决定加大对某种产品的研发投入,已知研发投入![]() (十万元)与利润
(十万元)与利润![]() (百万元)之间有如下对应数据:
(百万元)之间有如下对应数据:
| 2 | 3 | 4 | 5 | 6 |
| 2 | 4 | 5 | 6 | 7 |
若由资料知![]() 对
对![]() 呈线性相关关系。试求:
呈线性相关关系。试求:
(1)线性回归方程![]() ;
;
(2)估计![]() 时,利润是多少?
时,利润是多少?
附:利用“最小二乘法”计算a,b的值时,可根据以下公式:
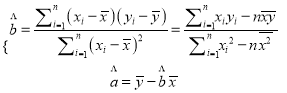
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=ax﹣1(a>0,且a≠1).
(1)求f(2)+f(﹣2)的值;
(2)求f(x)的解析式;
(3)解关于x的不等式f(x)<4,结果用集合或区间表示.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月产量如表(单位:辆):
轿车A | 轿车B | 轿车C | |
舒适型 | 100 | 150 | z |
标准型 | 300 | 450 | 600 |
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆。
(1)求z的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本。将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各组函数中,表示同一函数的是( )
A.f(x)=x﹣1,g(x)= ![]() ﹣1
﹣1
B.f(x)=|x|,g(x)=( ![]() )2
)2
C.f(x)=x,g(x)= ![]()
D.f(x)=2x,g(x)= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答
(1)已知幂函数f(x)=(﹣2m2+m+2)x﹣2m+1为偶函数,求函数f(x)的解析式;
(2)已知x+x﹣1=3(x>1),求x2﹣x﹣2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com