
【题目】如图,在菱形![]() 中,
中, ![]() ,
, ![]() ,以4个顶点为圆心的扇形的半径为1,若在该菱形中任意选取一点,该点落在阴影部分的概率为
,以4个顶点为圆心的扇形的半径为1,若在该菱形中任意选取一点,该点落在阴影部分的概率为![]() ,则圆周率
,则圆周率![]() 的近似值为( )
的近似值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】因为菱形的内角和为360°,
所以阴影部分的面积为半径为1的圆的面积,
故由几何概型可知 ,
,
解得![]() .选C。
.选C。
【题型】单选题
【结束】
12
【题目】已知函数f(x)= ,若g(x)=f(x)-a恰好有3个零点,则a的取值范围为( )
,若g(x)=f(x)-a恰好有3个零点,则a的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】给出下列四个命题中:
①命题: ![]() ;
;
②函数f(x)=2x﹣x2有三个零点;
③对(x,y)∈{(x,y)|4x+3y﹣10=0},则x2+y2≥4.
④已知函数 ![]() ,若△ABC中,角C是钝角,那么f(sinA)>f(cosB)
,若△ABC中,角C是钝角,那么f(sinA)>f(cosB)
其中所有真命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1) 把![]() 的图象上每一点的纵坐标变为原来的
的图象上每一点的纵坐标变为原来的![]() 倍,再将横坐标向右平移
倍,再将横坐标向右平移![]() 个单位,可得
个单位,可得![]() 图象,求
图象,求![]() ,
,![]() 的值;
的值;
(2) 若对任意实数![]() 和任意
和任意![]() ,恒有
,恒有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC﹣A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F分别是A1C1 , BC的中点. 
(1)证明:平面AEB⊥平面BB1C1C;
(2)证明:C1F∥平面ABE;
(3)设P是BE的中点,求三棱锥P﹣B1C1F的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】砂糖橘是柑橘类的名优品种,因其味甜如砂糖故名.某果农选取一片山地种植砂糖橘,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的![]() 倍.
倍.

(1)求a,b的值;
(2)从样本中产量在区间(50,60]上的果树里随机抽取两株,求产量在区间(55,60]上的果树至少有一株被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
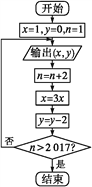
【题目】已知某算法的程序框图如图所示,若将输出的(x,y)值依次记为(x1,y1),(x2,y2),…,(xn,yn),…
(1)若程序运行中输出的一个数组是(9,t),求t的值.
(2)程序结束时,共输出(x,y)的组数为多少?
(3)写出程序框图的程序语句.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的奇函数f(x)的周期为4,且x∈(0,2)时f(x)=ln(x2﹣x+b),若函数f(x)在区间[﹣2,2]上恰有5个零点,则实数b应满足的条件是( )
A.﹣1<b≤1
B.﹣1<b<1或b= ![]()
C.![]() <b
<b ![]()
D.![]() <b≤1或b=
<b≤1或b= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均为正数的数列{an}的前n项和为Sn , 向量 ![]() =(Sn , an+1),
=(Sn , an+1), ![]() =(an+1,4)(n∈N*),且
=(an+1,4)(n∈N*),且 ![]() ∥
∥ ![]()
(1)求{an}的通项公式
(2)设f(n)=  bn=f(2n+4),求数列{bn}的前n项和Tn .
bn=f(2n+4),求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的命题个数是( )
①. 如果![]() 共面,
共面, ![]() 也共面,则
也共面,则![]() 共面;
共面;
②.已知直线a的方向向量![]() 与平面
与平面![]() ,若
,若![]() //
// ![]() ,则直线a//
,则直线a// ![]() ;
;
③若![]() 共面,则存在唯一实数
共面,则存在唯一实数![]() 使
使![]() ,反之也成立;
,反之也成立;
④.对空间任意点O与不共线的三点A、B、C,若![]() =x
=x![]() +y
+y![]() +z
+z![]()
(其中x、y、z∈R),则P、A、B、C四点共面.
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com