
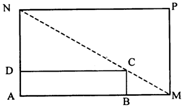
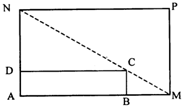
 某城市规划部门计划依托一矩形花园ABCD将之扩建成一个再大些的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知AB=3米,AD=2米.现有一飞鸟在矩形花园AMPN上空自由飞翔,并确定在花园AMPN内休息.
某城市规划部门计划依托一矩形花园ABCD将之扩建成一个再大些的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知AB=3米,AD=2米.现有一飞鸟在矩形花园AMPN上空自由飞翔,并确定在花园AMPN内休息.| 3 | 16 |
| 3 |
| 16 |
| ab |
| ND |
| DC |
| AN |
| AM |
| x-2 |
| 3 |
| x |
| AM |
| 3x |
| x-2 |
| SABCD |
| SAMPN |
| 6 | ||
|
| 2(x-2) |
| x2 |
| 2(x-2) |
| x2 |
| 3 |
| 16 |
| 8 |
| 3 |
| 3x2 |
| x-2 |
| 3(x-2)2+12(x-2)+12 |
| x-2 |
| 12 |
| x-2 |
| 36 |
| ab |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
 某城市自西向东和自南向北的两条主干道的东南方位有一块空地,市规划部门计划利用它建设一个供市民休闲健身的小型绿化广场,如下图所示是步行小道设计方案示意图,其中,Ox,Oy分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点O处修一条步行小道,小道为抛物线y=x2的一段,在小道上依次以点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(n≥10,n∈N*)为圆心,修一系列圆型小道,这些圆型小道与主干道Ox相切,且任意相邻的两圆彼此外切,若x1=1(单位:百米)且xn+1<xn.
某城市自西向东和自南向北的两条主干道的东南方位有一块空地,市规划部门计划利用它建设一个供市民休闲健身的小型绿化广场,如下图所示是步行小道设计方案示意图,其中,Ox,Oy分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点O处修一条步行小道,小道为抛物线y=x2的一段,在小道上依次以点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(n≥10,n∈N*)为圆心,修一系列圆型小道,这些圆型小道与主干道Ox相切,且任意相邻的两圆彼此外切,若x1=1(单位:百米)且xn+1<xn.| 1 |
| xn |
| πS |
查看答案和解析>>
科目:高中数学 来源:2014届湖北省高二9月调研考试理科数学试卷(解析版) 题型:解答题
(本小题满分14分)某城市自西向东和自南向北的两条主干道的东南方位有一块空地市规划部门计划利用它建设一个供市民休闲健身的小型绿化广场,如下图所示是步行小道设计方案示意图,

其中, 分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点
分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点 处修一条步行小道,小道为抛物线
处修一条步行小道,小道为抛物线 的一段,在小道上依次以点
的一段,在小道上依次以点
 为圆心,修一系列圆型小道,这些圆型小道与主干道
为圆心,修一系列圆型小道,这些圆型小道与主干道 相切,且任意相邻的两圆彼此外切,若
相切,且任意相邻的两圆彼此外切,若 (单位:百米)且
(单位:百米)且 .
.
(1)记以 为圆心的圆与主干道
为圆心的圆与主干道 切于
切于 点,证明:数列
点,证明:数列 是等差数列,并求
是等差数列,并求 关于
关于 的表达式;
的表达式;
(2)记 的面积为
的面积为 ,根据以往施工经验可知,面积为
,根据以往施工经验可知,面积为 的圆型小道的施工工时为
的圆型小道的施工工时为 (单位:周).试问5周时间内能否完成前
(单位:周).试问5周时间内能否完成前 个圆型小道的修建?请说明你的理由.
个圆型小道的修建?请说明你的理由.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省孝感高中高二(上)9月调考数学试卷(理科)(解析版) 题型:解答题
 为圆心,修一系列圆型小道,这些圆型小道与主干道Ox相切,且任意相邻的两圆彼此外切,若x1=1(单位:百米)且xn+1<xn.
为圆心,修一系列圆型小道,这些圆型小道与主干道Ox相切,且任意相邻的两圆彼此外切,若x1=1(单位:百米)且xn+1<xn. 是等差数列,并求|OAn|关于n的表达式;
是等差数列,并求|OAn|关于n的表达式; (单位:周).试问5周时间内能否完成前n个圆型小道的修建?请说明你的理由.
(单位:周).试问5周时间内能否完成前n个圆型小道的修建?请说明你的理由.
查看答案和解析>>
科目:高中数学 来源:江苏省如东县08-09学年高一下学期期末调研考试 题型:解答题
某城市规划部门计划依托一矩形花园 将之扩建成一个再大些的矩形花园
将之扩建成一个再大些的矩形花园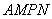 ,要求
,要求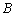 在
在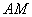 上,
上, 在
在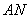 上,且对角线
上,且对角线 过
过 点,已知
点,已知 米,
米,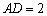 米.现有一飞鸟在矩形花园
米.现有一飞鸟在矩形花园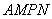 上空自由飞翔,并确定在花园
上空自由飞翔,并确定在花园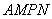 内休息.
内休息.
(1)要使飞鸟恰巧停在矩形花园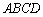 内的概率不大于
内的概率不大于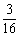 ,则
,则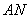 的长应在什么范围内?
的长应在什么范围内?
(2)当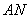 的长度是多少时,矩形
的长度是多少时,矩形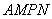 的面积最小?并求最小面积.
的面积最小?并求最小面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com