Question

方程lg（3-x）+lg（x-1）=lg（a-x）有两实数解，则实数a的取值范围为     ．

Answer 1

【答案】分析：先利用对数的运算性质把原方程转化为（x-1）（3-x）=a-x，再将方程的解转化为图象的交点，利用图象解题即可．
解答：解：当
即1＜x＜3时，原方程为（x-1）（3-x）=a-x，即a=-x²+5x-3．
作出函数y=-x²+5x-3（1＜x＜3）的图象．
显然，该图象与直线y=a的交点的横坐标是原方程的解．
由图象看出：
当3＜a＜时，原方程有两解；
当1＜a≤3或时，原方程有一解；
当a＞或a≤1时原方程无解．
故答案为3＜a＜．
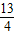
点评：本题利用转化的思想把方程的解转化为图象的交点，用利用图形找到结论．利用图形的好处是直观，形象，容易得结论．