
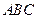 ,
,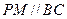 ,PA = PC,
,PA = PC,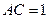 ,
,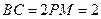 ,
, ,若该几何体左视图(侧视图)的面积为
,若该几何体左视图(侧视图)的面积为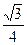 .
.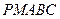 的体积V.
的体积V.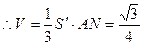
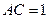 ,BC=2,
,BC=2,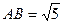 ,
,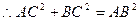 ,∴
,∴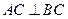 , …………2分
, …………2分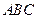 ,平面PAC∩平面
,平面PAC∩平面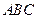 =AC,
=AC,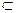 平面PAC, ∴PA⊥BC. …………4分
平面PAC, ∴PA⊥BC. …………4分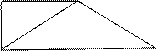 …………6分
…………6分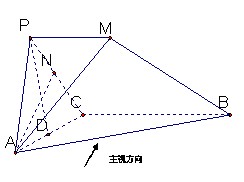
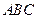 ,则PD⊥平面ABC,
,则PD⊥平面ABC, =
=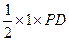 =
=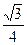 .
.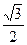 ,并易知
,并易知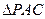 是边长为1的正三角形,…………8分
是边长为1的正三角形,…………8分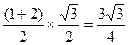 . …………10分
. …………10分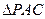 是边长为1的正三角形,可知AN⊥PC,
是边长为1的正三角形,可知AN⊥PC,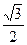 ,…………12分
,…………12分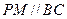 可知四边形PCBM是上、下底边长分别为1和2,PC的长1为高的
可知四边形PCBM是上、下底边长分别为1和2,PC的长1为高的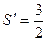 .
.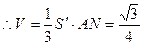 .…………14分
.…………14分

 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
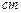 ), 则按图中尺寸,做成的工作台用去的合板的
), 则按图中尺寸,做成的工作台用去的合板的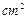 。(制作过程合板损耗和合板厚度忽略不计)
。(制作过程合板损耗和合板厚度忽略不计)查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
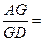

 2”。若把该结论推广到空间,则有结论:“在棱长都相等的四面体
2”。若把该结论推广到空间,则有结论:“在棱长都相等的四面体 中,若
中,若 的中心为
的中心为 ,四面体内部一点
,四面体内部一点 到四面体各面的距离都相等,则
到四面体各面的距离都相等,则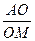 = 。
= 。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com