
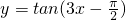 的周期是
的周期是 ;
;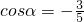 ;
;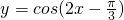 的图象的一个对称中心是
的图象的一个对称中心是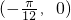 ;
;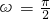 .
. ,可得②错误;对于③、根据余弦函数的性质,求出
,可得②错误;对于③、根据余弦函数的性质,求出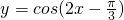 的对称中心的坐标,进而分析可得③正确;对于④、根据题意,分析可得f(x+4)=-f(x+2)=f(x),则函数f(x)的周期为4,由周期求法可得ω=±
的对称中心的坐标,进而分析可得③正确;对于④、根据题意,分析可得f(x+4)=-f(x+2)=f(x),则函数f(x)的周期为4,由周期求法可得ω=± ,则④错误;综合可得答案.
,则④错误;综合可得答案.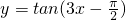 的周期是
的周期是 ,①正确;
,①正确;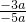 =
= ,②错误;
,②错误;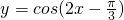 中,有2x-
中,有2x- =kπ+
=kπ+ ,解可得x=
,解可得x= +
+ ,其对称中心的坐标为(
,其对称中心的坐标为( +
+ ,0),
,0),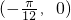 ,则③正确;
,则③正确;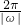 =4,则ω=±
=4,则ω=± ,则④错误;
,则④错误;

科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 3 |
| 3 |
| 5 |
| π |
| 3 |
| π |
| 12 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| 1+|x| |
| x |
| 1+n|x| |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河南省毕业班高三高考适应性考试数学理卷 题型:选择题
给出定义:若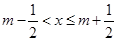 (其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m在此基础上给出下列关于函数
(其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m在此基础上给出下列关于函数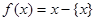 的四个命题:
的四个命题:
①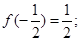 ②
②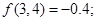
③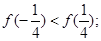 ④
④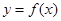 的定义域为R,值域是
的定义域为R,值域是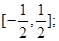
则其中真命题的序号是 ( )
A.①② B.①③ C.②④ D.③④
第Ⅱ卷
查看答案和解析>>
科目:高中数学 来源: 题型:
①函数![]() 的极小值只有f(-2)=-17,f(1)=10,极大值为f(0)=15;
的极小值只有f(-2)=-17,f(1)=10,极大值为f(0)=15;
②函数![]() 的极小值只有f(-1)=2,f(1)=10,极大值为f(0)=15;
的极小值只有f(-1)=2,f(1)=10,极大值为f(0)=15;
③函数![]() 的极大值为f(2)=47,极小值为f(0)=15,f(-2)=-17;
的极大值为f(2)=47,极小值为f(0)=15,f(-2)=-17;
④函数![]() 的极大值为f(-2)=-17,f(1)=10,极小值为f(-1)=2.
的极大值为f(-2)=-17,f(1)=10,极小值为f(-1)=2.
其中正确命题的个数是( )
A.1 B.2
C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com