练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】有一解三角形的题目因纸张破损，有一条件不清，具体如下：在△ABC中，已知a= ，2cos2 =（ ﹣1）cosB，c= ， 求角A，若该题的答案是A=60°，请将条件补充完整．

    【答案】
    【解析】解：在△ABC中，∵已知a= ，2cos2 =（ ﹣1）cosB，
    ∴1+cos（A+C）=（ ﹣1）cosB，
    即 1﹣cosB=（ ﹣1）cosB，∴cosB= ，∴B= ．
    若A=60°，则C=180°﹣A﹣B=75°，sin75°=sin（45°+30°）=sin45°cos30°+cos45°sin30°= ，
    则由正弦定理可得 = ，求得c= ，
    所以答案是： ．
    【考点精析】关于本题考查的余弦定理的定义，需要了解余弦定理:;;才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】己知全集 U=R，集合 A={x|3≤x＜7}，B={x|2＜log2 x＜4}．
    （1）求A∪B；
    （2）求（UA ）∩B．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C1、抛物线C2的焦点均在x轴上，C1的中心和C2的顶点均为原点O，从每条曲线上取两个点，将其坐标记录于下表中：

    x

    3

    ﹣2

    4

    y

    ﹣2

    0

    ﹣4


    （1）求C1、C2的标准方程；
    （2）请问是否存在直线l满足条件：①过C2的焦点F；②与C1交不同两点M、N且满足 ？若存在，求出直线l的方程；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准（吨），一位居民的月用水量不超过的部分按平价收费，超过的部分按议价收费.为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照， ， ， 分成9组，制成了如图所示的频率分布直方图.

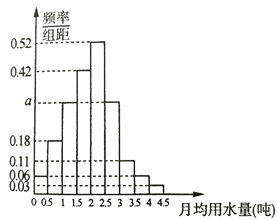
    （Ⅰ）求直方图中的值；

    （Ⅱ）若将频率视为概率，从该城市居民中随机抽取3人，记这3人中月均用水量不低于3吨的人数为，求的分布列与数学期望.

    （Ⅲ）若该市政府希望使85%的居民每月的用水量不超过标准（吨），估计的值（精确到0.01），并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，将一个各面都涂了油漆的正方体，切割为125个同样大小的小正方体，经过搅拌后，从中随机取一个小正方体，记它的涂漆面数为X，则X的均值E（X）=（ ）

    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在锐角△ABC中，a、b、c分别为角A、B、C所对的边，且 =2csinA
    （1）确定角C的大小；
    （2）若c= ，且△ABC的面积为 ，求a+b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知 =（2，1）， =（1，7）， =（5，1），设Z是直线OP上的一动点．

    （1）求使 取最小值时的 ；
    （2）对（1）中求出的点Z，求cos∠AZB的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列叙述正确的个数是（ ）
    ①若a＞b，则ac2＞bc2；
    ②若命题p为真命题题，命题q为假命题，则p∨q为假命题；
    ③若命题p：x0∈R，x ﹣x0+1≤0，则￢p：x∈R，x2﹣x+1＞0．
    A.0
    B.1
    C.2
    D.3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，内角A，B，C的对边分别为a，b，c，已知2ccosA+a=2b
    （1）求角C的值；
    （2）若c=2，且△ABC的面积为 ，求a，b．

    查看答案和解析>>

    同步练习册答案