Question

设函数f（x）=

1-|x-1|，x＜2 1 2 f(x-2)，x≥2

，则函数F（x）=xf（x）-1的零点的个数为

6

．

Answer 1

分析：由F（x）=xf（x）-1=0，得f（x）=

1

x

，设y=f（x）与y=

1

x

，在同一坐标系中分别画出两个函数图象，由图象即可求出两个函数的交点个数，即函数F（x）=xf（x）-1的零点个数．

解答：解：∵F（x）=xf（x）-1，
∴由F（x）=xf（x）-1=0，
得f（x）=

1

x

，
设y=f（x）与y=

1

x

，在同一坐标系中分别画出两个函数图象，由图象即可求出两个函数的交点个数，即函数F（x）=xf（x）-1的零点个数．
作出函数y=f（x）与y=g（x）=

1

x

的图象如图：
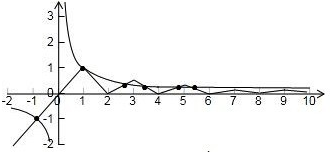
当x＜0时，y=f（x）单调递增，y=

1

x

为减函数，此时函数f（x）与y=g（x）=

1

x

只有一个交点．
∵f（1）=1，g（1）=1，∴f（1）=g（1），此时x=1是函数的一个零点．
∵f（3）=

1

2

f(1)=

1

2

，g（3）=

1

3

，满足f（3）＞g（3），∴此时在（2，4）内有两个交点．
∵f（5）=

1

2

f（3）=

1

4

，g（5）=

1

5

，满足f（5）＞g（5），∴此时在（4，6）内有两个交点，
∵f（7）=

1

2

f（5）=

1

8

，g（7）=

1

7

，满足f（7）＜g（7），∴此时在（6，8）内没有交点，
∵f（9）=

1

2

f(7)=

1

16

，g（9）=

1

9

，满足f（9）＜g（9），∴此时在（8，10）内有没有交点，
即当n＞7时，恒有f（x）＜g（x），此时，两个函数没有交点．
综上两个函数的交点个数为6个．
即函数F（x）=xf（x）-1的零点的个数为6个．
故答案为：6．

点评：本题主要考查函数零点的判定定理，将求函数零点的问题转化为求两个函数图象交点的问题是解答本题的关键．