
分析 基本事件总数为:n=${A}_{5}^{5}$=120,由五位数是波形数,知a2>a1、a3 ;a4>a3、a5,从而a2只能是3、4、5.由此利用分类讨论思想求出满足条件的五位数有2(A22+A33)个,由此能求出结果.
解答 解:由1,2,3,4,5组成一个没有重复数字的五位数,
基本事件总数为:n=${A}_{5}^{5}$=120,
∵五位数是波形数,
∴a2>a1、a3;a4>a3、a5,∴a2只能是3、4、5.
①若a2=3,则a4=5,a5=4,a1与a3是1或2,这时共有A22=2个符合条件的五位数.
②若a2=4,则a4=5,a1、a3、a5可以是1、2、3,共有A33=6个符合条件的五位数.
③若a2=5,则a4=3或4,此时分别与(1)(2)情况相同.
∴满足条件的五位数有:m=2(A22+A33)=16个,
∴由1,2,3,4,5组成一个没有重复数字的五位数是波形数的概率是p=$\frac{m}{n}=\frac{16}{120}=\frac{2}{15}$.
故答案为:$\frac{2}{15}$.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意分类讨论思想的合理运用.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-5)2+(y-4)2=16 | B. | (x+5)2+(y-4)2=16 | C. | (x-5)2+(y-4)2=25 | D. | (x+5)2+(y-4)2=25 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4031 | B. | 4032 | C. | 4033 | D. | 4034 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
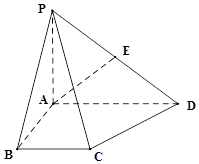 四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=90°,AD∥BC,AB=BC=2,AD=4,PA⊥底面ABCD,PD与底面ABCD成30°角,E是PD的中点.
四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=90°,AD∥BC,AB=BC=2,AD=4,PA⊥底面ABCD,PD与底面ABCD成30°角,E是PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com