
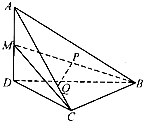
 如图,在四面 体ABCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2$\sqrt{2}$,M是AD的中点,P是BM的中点,点Q在线段AC 上,且AQ=3QC.
如图,在四面 体ABCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2$\sqrt{2}$,M是AD的中点,P是BM的中点,点Q在线段AC 上,且AQ=3QC.分析 (1)过P做PH∥AD,交BD于H,过Q作QS∥AD,交DC于S,则PH平行且等于$\frac{1}{4}$AD,QC平行且等于$\frac{1}{4}$AD,证明PQ∥HS,利用AD⊥平面BCD,AD⊥HS,即可证明结论;
(2)证明∠ACD为直线CD与平面ACB所成角的大小,即可求解;
(3)利用反证法进行判断即可.
解答  (1)证明:过P做PH∥AD,交BD于H,过Q作QS∥AD,交DC于S,则PH平行且等于$\frac{1}{4}$AD,QC平行且等于$\frac{1}{4}$AD,∴PH平行且等于QS,
(1)证明:过P做PH∥AD,交BD于H,过Q作QS∥AD,交DC于S,则PH平行且等于$\frac{1}{4}$AD,QC平行且等于$\frac{1}{4}$AD,∴PH平行且等于QS,
∴QSHP为平行四边形,
∴PQ∥HS,
∵AD⊥平面BCD,
∴AD⊥HS,
∴PQ⊥AD;
(2)解:在△ADC中,做DN⊥AC于N,则
∵DN⊥BC,BC∩AC=C,
∴DN⊥平面ACB.
∴∠ACD为直线CD与平面ACB所成角的大小.
∵AD=2,BD=2$\sqrt{2}$,∠BDC=45°,
∴AD=DC,
∴∠ACD=45°,
∴直线CD与平面ACB所成角的大小为45°;
(3)解:不存在.假设存在点E,使得平面CPE⊥平面CMB,交线为CP,过B作CP的垂线,垂足为F,可得F在CP的延长线上,F在下底面上射影N在CH的延长线上,可得BH=$\frac{\sqrt{357}}{18}$>1,∠CDN为钝角,从而过C做BD垂线,E在DB的延长线上,而不能在线段上.
点评 本题考查线面垂直的性质,考查线面角,考查平面与平面垂直,考查学生分析解决问题的能力,属于中档题.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平行于同一直线的两直线平行 | |
| B. | 垂直于同一直线的两直线平行 | |
| C. | 平行于同一平面的两平面不一定平行 | |
| D. | 垂直于同一平面的两平面平行 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com