
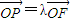 ,
,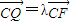 (λ≠0).
(λ≠0).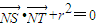 ,试求出r的值.
,试求出r的值.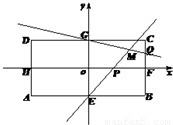
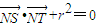 ,得|NS||NT|=|ON|2,又由ON⊥ST,得OS⊥OT,设S(x1,y1),T(x2,y2),则x1x2+y1y2=0(*),设直线ST:y=kx+m(m≠±2),与椭圆方程联立消掉y得x的二次方程,把韦达定理代入(*得)式得关于k,m的方程;再由直线ST与圆相切得r=
,得|NS||NT|=|ON|2,又由ON⊥ST,得OS⊥OT,设S(x1,y1),T(x2,y2),则x1x2+y1y2=0(*),设直线ST:y=kx+m(m≠±2),与椭圆方程联立消掉y得x的二次方程,把韦达定理代入(*得)式得关于k,m的方程;再由直线ST与圆相切得r=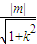 ,两方程联立即可求得r值;
,两方程联立即可求得r值; -2,直线GQ的方程为y=-
-2,直线GQ的方程为y=-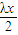 +2,
+2,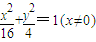 .
.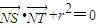 ,得|NS||NT|=|ON|2,又ON⊥ST,则OS⊥OT,
,得|NS||NT|=|ON|2,又ON⊥ST,则OS⊥OT,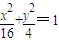 得(1+4k2)x2+8kmx+4m2-16=0,
得(1+4k2)x2+8kmx+4m2-16=0,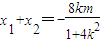 ,
,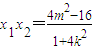 .
.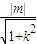 ②,
②,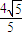 ∈(0,2).
∈(0,2).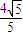 .
.

科目:高中数学 来源: 题型:
 如图,在矩形ABCD中,AB=2BC,P,Q分别为线段AB,CD的中点,EP⊥平面ABCD.
如图,在矩形ABCD中,AB=2BC,P,Q分别为线段AB,CD的中点,EP⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在矩形ABCD中,已知AB=2AD=4,E为AB的中点,现将△AED沿DE折起,使点A到点P处,满足PB=PC,设M、H分别为PC、DE的中点.
如图,在矩形ABCD中,已知AB=2AD=4,E为AB的中点,现将△AED沿DE折起,使点A到点P处,满足PB=PC,设M、H分别为PC、DE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在矩形ABCD中,AB=3
如图,在矩形ABCD中,AB=3| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系:
如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系:查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在矩形ABCD中,AB=
如图,在矩形ABCD中,AB=| 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com