分析:(1)要证数列{an}是等比数列,只需证明数列{an}的后一项比前一项是常数即可,可先对y=x2求导数,y=x2在切点处的导数,就是在该点处的切线的斜率,求出切线方程,就可找到切点在x轴上的投影的横坐标,再求相邻横坐标之商,看是否为常数,就可证出数列{an}是等比数列,再根据等比数列的通项公式求数列{an}的通项公式即可.
(2)根据(1)中所求数列{an}的通项公式求出数列{bn}的通项公式,再用错位相减求前n项和Sn
解答:解:(1)对y=x
2求导数,得y'=2x,切点是M
n(a
n,a
n2)的切线方程是y-a
n2=2a
n(x-a
n).(2分)
当n=1时,切线过点P(1,0),即0-a
12=2a
1(1-a
1),得a
1=2;
当n>1时,切线过点
Pn-1(an-1,0),即0-=2an(an-1-an),得=2所以数列{a
n}是首项a
1=2,公比为2的等比数列.
所以数列{a
n}的通项公式为a
n=2
n,n∈N
*(6分)
(2)∵
bn=,a
n=2
n,∴
bn=S
n=
+
+
+…+
①
2S
n=
+
+…+
+
②
①-②,得-S
n=
+
+
+…+
-
=
-
=1-
-
=1-
点评:本题考查了等比数列的证明,以及错位相减求和.



 阅读快车系列答案
阅读快车系列答案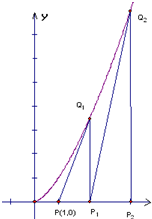 如图,过点P(1,0)作曲线C:y=xk(x∈(0,+∞),k∈N*,k>1)的切线,切点为Q1,设Q1点在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,…,Qn,…,设点Qn的横坐标为an.
如图,过点P(1,0)作曲线C:y=xk(x∈(0,+∞),k∈N*,k>1)的切线,切点为Q1,设Q1点在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,…,Qn,…,设点Qn的横坐标为an.

 (2009•锦州一模)过点P(1,0)作曲线C:y=x2(x>0)的切线,切点为Q1,没Q1在x轴上的投影是P1,又过P1,作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2…,依次下去,得到一系列点Q1Q2,…Qn,设Qn的横坐标为an.
(2009•锦州一模)过点P(1,0)作曲线C:y=x2(x>0)的切线,切点为Q1,没Q1在x轴上的投影是P1,又过P1,作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2…,依次下去,得到一系列点Q1Q2,…Qn,设Qn的横坐标为an.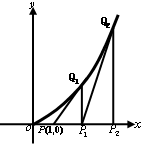 (2013•韶关二模)如图,过点P(1,0)作曲线C:y=x2(x∈(0,+∞))的切线,切点为Q1,设点Q1在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,Q3-Qn,设点Qn的横坐标为an.
(2013•韶关二模)如图,过点P(1,0)作曲线C:y=x2(x∈(0,+∞))的切线,切点为Q1,设点Q1在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,Q3-Qn,设点Qn的横坐标为an.