
分析 求出|OA|,P点到OA的距离,利用平行四边形OBPA的面积为3,求出a,可得c,即可求出双曲线的离.
解答 解:双曲线的渐近线方程是:3x±ay=0,设P(m,n)是双曲线上任一点,
过P平行于OB:3x+ay=0的方程是:3x+ay-3m-an=0,
联立$\left\{\begin{array}{l}{3x-ay=0}\\{3x+ay-3m-an=0}\end{array}\right.$,得两直线交点A($\frac{3m+an}{6},\frac{3m+an}{2a}$),
|OA|=$\sqrt{(\frac{3m+an}{6})^{2}+(\frac{3m+an}{2a})^{2}}$=$\frac{|3m+an|\sqrt{{a}^{2}+9}}{6a}$,
P点到OA的距离是:d=$\frac{|3m-an|}{\sqrt{{a}^{2}+9}}$,
∵|OA|•d=1,
∴$\frac{|3m+an|\sqrt{{a}^{2}+9}}{6a}•\frac{|3m-an|}{\sqrt{{a}^{2}+9}}=3$,即$\frac{|9{m}^{2}-{a}^{2}{n}^{2}|}{6a}=3$,
∵9m2-a2n2=9a2,
∴a=2,则c=$\sqrt{4+9}=\sqrt{13}$,
∴e=$\frac{\sqrt{13}}{2}$.
故答案为:$\frac{\sqrt{13}}{2}$.
点评 本题考查双曲线的方程与性质,考查学生的计算能力,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,ex-x-1>0 | B. | ?x∉R,ex-x-1>0 | C. | ?x∈R,ex-x-1≥0 | D. | ?x∈R,ex-x-1>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
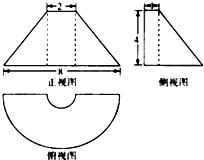 如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于( )
如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于( )| A. | 12π | B. | 16π | C. | 20π | D. | 24π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com