
 如图ABC-A1B1C1是直三棱柱,底面△ABC是等腰直角三角形,且AB=AC=4,直三棱柱的高等于4,线段B1C1的中点为D,线段BC的中点为E,线段CC1的中点为F.
如图ABC-A1B1C1是直三棱柱,底面△ABC是等腰直角三角形,且AB=AC=4,直三棱柱的高等于4,线段B1C1的中点为D,线段BC的中点为E,线段CC1的中点为F.分析 (1)以A为原点建立空间坐标系,求出$\overrightarrow{AD}$,$\overrightarrow{EF}$的坐标,利用向量的夹角公式得出AD,EF的夹角;
(2)证明AE⊥平面DEF,求出AE和S△DEF,代入体积公式计算.
解答  解:(1)以A为坐标原点,AB、AC、AA1分别为x轴,y轴,z轴建立空间直角坐标系.
解:(1)以A为坐标原点,AB、AC、AA1分别为x轴,y轴,z轴建立空间直角坐标系.
依题意有D(2,2,4),A(0,0,0),E(2,2,0),F(0,4,2),
所以$\overrightarrow{AD}=(2,2,4)\overrightarrow{,EF}=(-2,2,2)$.
设异面直线AD、EF所成角为α,则$cosα=\frac{{|\overrightarrow{AD}\overrightarrow{•EF}|}}{{|\overrightarrow{AD}|•|\overrightarrow{EF}|}}$=$\frac{|-4+4+8|}{{\sqrt{4+4+16}•\sqrt{4+4+4}}}$=$\frac{{\sqrt{2}}}{3}$,
所以$α=arccos\frac{{\sqrt{2}}}{3}$,
即异面直线AD、EF所成角的大小为$arccos\frac{{\sqrt{2}}}{3}$.
(2)∵AB=AC=4,AB⊥AC,∴$BC=4\sqrt{2}$,$AE=2\sqrt{2}$,DE=AA1=4,
∴S△DEF=$\frac{1}{2}×4×2\sqrt{2}$=4$\sqrt{2}$,
由E为线段BC的中点,且AB=AC,
∴AE⊥BC,
又BB1⊥面ABC,∴AE⊥BB1,
∴AE⊥面BB1C1C,
∴${V_{D-AEF}}={V_{A-DEF}}=\frac{1}{3}{S_{△DEF}}•AE=\frac{1}{3}•4\sqrt{2}•2\sqrt{2}=\frac{16}{3}$,
∴三棱锥D-AEF的体积为$\frac{16}{3}$.
点评 本题考查了异面直线所成的角,棱锥的体积计算,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 三条侧棱两两垂直的正三棱锥,其俯视图如图所示,主视图的边界是底边长为2的等腰三角形,则主视图的面积等于$\frac{{\sqrt{6}}}{3}$.
三条侧棱两两垂直的正三棱锥,其俯视图如图所示,主视图的边界是底边长为2的等腰三角形,则主视图的面积等于$\frac{{\sqrt{6}}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
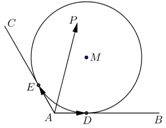 如图所示,∠BAC=$\frac{2π}{3}$,圆M与AB,AC分别相切于点D,E,AD=1,点P是圆M及其内部任意一点,且$\overrightarrow{AP}=x\overrightarrow{AD}+y\overrightarrow{AE}$(x,y∈R),则x+y的取值范围是( )
如图所示,∠BAC=$\frac{2π}{3}$,圆M与AB,AC分别相切于点D,E,AD=1,点P是圆M及其内部任意一点,且$\overrightarrow{AP}=x\overrightarrow{AD}+y\overrightarrow{AE}$(x,y∈R),则x+y的取值范围是( )| A. | $[1,4+2\sqrt{3}]$ | B. | $[4-2\sqrt{3},4+2\sqrt{3}]$ | C. | $[1,2+\sqrt{3}]$ | D. | $[2-\sqrt{3},2+\sqrt{3}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
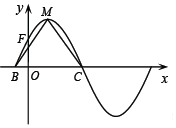 函数f(x)=2sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,M为最高点,该图象与y轴交于点F(0,$\sqrt{2}$),与x轴交于点B,C,且△MBC的面积为π.
函数f(x)=2sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,M为最高点,该图象与y轴交于点F(0,$\sqrt{2}$),与x轴交于点B,C,且△MBC的面积为π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com