
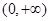 ,若对给定的正数K,定义
,若对给定的正数K,定义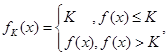 则当函数
则当函数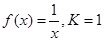 时,
时, 
科目:高中数学 来源:不详 题型:解答题
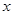 万件,需另投入流动成本为
万件,需另投入流动成本为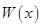 万元,在年产量不足8万件时,
万元,在年产量不足8万件时,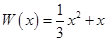 (万元),在年产量不小于8万件时,
(万元),在年产量不小于8万件时,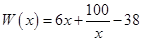 (万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.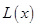 (万元)关于年产量
(万元)关于年产量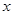 (万件)的函数解析式;
(万件)的函数解析式;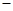 固定成本
固定成本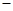 流动成本)
流动成本)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.1800 | B.1700 | C.1600 | D.1500 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
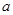 的正方形铁片,铁片的四角截去四个边长均为
的正方形铁片,铁片的四角截去四个边长均为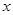 的小正方形,然后做成一个无盖方盒。
的小正方形,然后做成一个无盖方盒。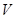 表示为
表示为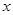 的函数;(2)
的函数;(2)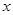 多大时,方盒的容积
多大时,方盒的容积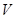 最大?
最大?查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 在区间
在区间 上有定义, 若
上有定义, 若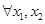
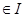 , 都有
, 都有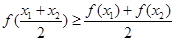 , 则称
, 则称 是区间
是区间 的向上凸函数;若
的向上凸函数;若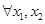
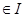 , 都有
, 都有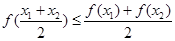 , 则称
, 则称 是区间
是区间 的向下凸函数. 有下列四个判断:
的向下凸函数. 有下列四个判断: 是区间
是区间 的向上凸函数,则
的向上凸函数,则 是区间
是区间 的向下凸函数;
的向下凸函数; 和
和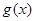 都是区间
都是区间 的向上凸函数, 则
的向上凸函数, 则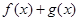 是区间
是区间 的向上凸函数;
的向上凸函数; 在区间
在区间 的向下凸函数且
的向下凸函数且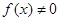 ,则
,则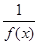 是区间
是区间 的向上凸函数;
的向上凸函数; 是区间
是区间 的向上凸函数,
的向上凸函数,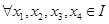 , 则有
, 则有
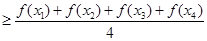
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com