
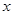 万件,需另投入流动成本为
万件,需另投入流动成本为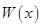 万元,在年产量不足8万件时,
万元,在年产量不足8万件时,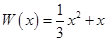 (万元),在年产量不小于8万件时,
(万元),在年产量不小于8万件时,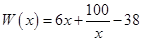 (万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.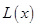 (万元)关于年产量
(万元)关于年产量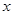 (万件)的函数解析式;
(万件)的函数解析式;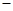 固定成本
固定成本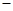 流动成本)
流动成本) 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:高中数学 来源:不详 题型:解答题
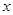 次之间的关系为Z=
次之间的关系为Z=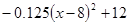 ,1≤
,1≤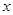 ≤16,且
≤16,且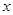 为整数,试问该服装第几周出售时,每件销售利润最大?最大利润为多少?
为整数,试问该服装第几周出售时,每件销售利润最大?最大利润为多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
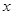 元/千克,政府补贴为
元/千克,政府补贴为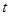 元/千克,根据市场调查,当
元/千克,根据市场调查,当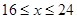 时,这种食品市场日供应量
时,这种食品市场日供应量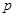 万千克与市场日需量
万千克与市场日需量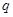 万千克近似地满足关系:
万千克近似地满足关系: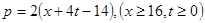 ,
,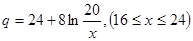 。当
。当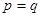 市场价格称为市场平衡价格。
市场价格称为市场平衡价格。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com