[3,+∞) 2 3
分析:A.通过作出函数y=|x+1|+|x-2|的图象求出函数的最小值,然后结合图象可知a的取值范围;
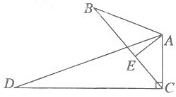
B.先证明Rt△ABE∽Rt△ADC,然后根据相似建立等式关系,求出所求即可;
C.先根据ρ
2=x
2+y
2,sin
2+cos
2θ=1将极坐标方程和参数方程化成直角坐标方程,根据当两点连线经过两圆心时|AB|的最小,从而最小值为两圆心距离减去两半径.
解答:
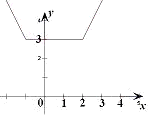
解:A.先作出函数y=|x+1|+|x-2|的图象,可知函数的最小值为3,故当a∈[3,+∞)上不等式a≥|x+1|+|x-2|存在实数解,
故答案为:[3,+∞)
B.∵∠B=∠D,AE⊥BC,∠ACD=90°
∴Rt△ABE∽Rt△ADC
而AB=6,AC=4,AD=12,
根据AD•AE=AB•AC解得:AE=2,
故答案为:2
C.
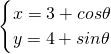
消去参数θ得,(x-3)
2+(y-4)
2=1
而p=1,则直角坐标方程为x
2+y
2=1,点A在圆(x-3)
2+(y-4)
2=1上,点B在圆x
2+y
2=1上
则|AB|的最小值为5-1-1=3
故答案为:3
点评:本题主要考查了绝对值函数,以及三角形相似和圆的参数方程等有关知识,同时考查了转化与划归的思想,属于基础题.

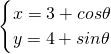 (θ为参数)和曲线C1:p=1上,则|AB|的最小值为________.
(θ为参数)和曲线C1:p=1上,则|AB|的最小值为________. 解:A.先作出函数y=|x+1|+|x-2|的图象,可知函数的最小值为3,故当a∈[3,+∞)上不等式a≥|x+1|+|x-2|存在实数解,
解:A.先作出函数y=|x+1|+|x-2|的图象,可知函数的最小值为3,故当a∈[3,+∞)上不等式a≥|x+1|+|x-2|存在实数解,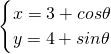 消去参数θ得,(x-3)2+(y-4)2=1
消去参数θ得,(x-3)2+(y-4)2=1

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 三选一题(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
三选一题(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (本题为选做题,请在下列三题中任选一题作答)
(本题为选做题,请在下列三题中任选一题作答) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)