
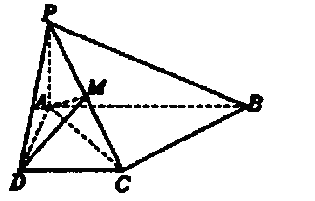
如图,已知四棱锥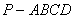 中,
中,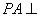 平面
平面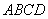 ,底面
,底面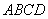 是直角梯形,且
是直角梯形,且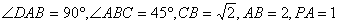 .
.
(1)求证: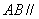 平面
平面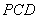 ;
;
(2)求证: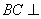 平面
平面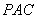 ;
;
(3)若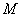 是
是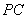 的中点,求三棱锥
的中点,求三棱锥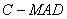 的体积.
的体积.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知函数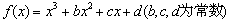 ,当
,当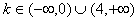 时,
时,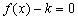 只有一个实数根;当
只有一个实数根;当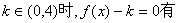 3个相异实根,现给出下列4个命题:
3个相异实根,现给出下列4个命题:
①函数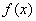 有2个极值点; ②函数
有2个极值点; ②函数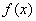 有3个极值点;
有3个极值点;
③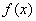 =4,
=4, =0有一个相同的实根; ④
=0有一个相同的实根; ④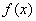 =0和
=0和 =0有一个相同的实根.
=0有一个相同的实根.
其中正确命题的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则实数a的取值范围是 ( )
A.(-1,2) B.(-∞,-3)∪(6,+∞) C.(-3,6) D.(-∞,-1)∪(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
在△ABC中,若a、b、c分别为角A,B,C的对边,且cos2B+cosB+cos(A-C)=1,则有
A.a、c、b成等比数列 B.a、c、b成等差数列
C.a、b、c成等差数列 D.a、b、c成等比数列
查看答案和解析>>
科目:高中数学 来源: 题型:
.下列关于回归分析的说法中错误的是 ( )
A. 回归直线一定过样本中心( )
)
B. 残差图中残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适
C. 两个模型中残差平方和越小的模型拟合的效果越好
D.甲、乙两个模型的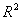 分别约为
分别约为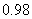 和
和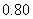 ,则模型乙的拟合效果更好
,则模型乙的拟合效果更好
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com