
【题目】设![]() 是
是![]() 的十进制写法中最后一个非零数字.证明:0·
的十进制写法中最后一个非零数字.证明:0·![]() …是无理数.
…是无理数.
【答案】见解析
【解析】
设![]() 是有理数.则存在
是有理数.则存在![]() 、
、![]() ,使得对每个
,使得对每个![]() ,均有
,均有![]() .
.
首先证明:存在![]() ,
,![]() ,且
,且![]() 的最后一个非零数字为1.
的最后一个非零数字为1.
事实上,设![]() ,其中,
,其中,![]() 、
、![]() ,
,![]() 不被2与5整除.
不被2与5整除.
则![]() 的最后一个非零数字为奇数,且不等于5.
的最后一个非零数字为奇数,且不等于5.
若其等于1,则取![]() ;若其等于3,则取
;若其等于3,则取![]() ;
;
若其等于7,则取![]() ;若其等于9,则取
;若其等于9,则取![]() .
.
在以上情形下,![]() 的最后一位非零数字分别与1、21、21、81的相同.
的最后一位非零数字分别与1、21、21、81的相同.
这样就求出了当![]() 时使得
时使得![]() 的数
的数![]() .
.
其次证明:对任意的![]() ,
,![]() .
.
事实上,记![]() 表示不超过实数
表示不超过实数![]() 的最大整数.
的最大整数.
则在![]() 的素因子分解式中,2的幂指数为
的素因子分解式中,2的幂指数为![]() ,
,
5的幂指数为![]() .
.
因为当![]() 时,
时,![]() ,所以,
,所以,![]() ,且
,且![]() ,
,
其中,![]() ,不被2与5整除.从而,其最后一位非零数字与
,不被2与5整除.从而,其最后一位非零数字与![]() 的相同.
的相同.
于是,不等于5,即最后取充分大的![]() ,使得
,使得![]() .
.
记![]() .则
.则![]() .
.
故![]() .
.
因此,![]() .
.
因为![]() ,所以,
,所以,![]() .
.
从而,![]() .
.
故
![]()
![]() ,
,
即![]() 与
与![]() 的最后一位数字
的最后一位数字![]() 相同.
相同.
另一方面,![]() ,但是,因为
,但是,因为![]() ,所以,
,所以,![]() 的最后一位数字不等于
的最后一位数字不等于![]() .
.
从而,![]() ,矛盾.
,矛盾.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心为坐标原点O,焦点在y轴上,离心率![]() ,椭圆上的点到焦点的最短距离为
,椭圆上的点到焦点的最短距离为![]() , 直线l与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且
, 直线l与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且![]() .
.
(1)求椭圆方程;
(2)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() .
.

(1)过![]() 作截面与线段
作截面与线段![]() 交于点H,使得
交于点H,使得![]() 平面
平面![]() ,试确定点H的位置,并给出证明;
,试确定点H的位置,并给出证明;
(2)在(1)的条件下,若二面角![]() 的大小为
的大小为![]() ,试求直线
,试求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大型综艺节目《最强大脑》中,有一个游戏叫做盲拧魔方,就是玩家先观察魔方状态并进行记忆,记住后蒙住眼睛快速还原魔方,盲拧在外人看来很神奇,其实原理是十分简单的,要学会盲拧也是很容易的.为了解某市盲拧魔方爱好者的水平状况,某兴趣小组在全市范围内随机抽取了![]() 名魔方爱好者进行调查,得到的情况如表所示:
名魔方爱好者进行调查,得到的情况如表所示:
用时(秒) |
|
|
|
|
男性人数 | 15 | 22 | 14 | 9 |
女性人数 | 5 | 11 | 17 | 7 |
附: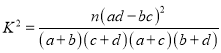 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
(1)将用时低于![]() 秒的称为“熟练盲拧者”,不低于
秒的称为“熟练盲拧者”,不低于![]() 秒的称为“非熟练盲拧者”.请根据调查数据完成以下
秒的称为“非熟练盲拧者”.请根据调查数据完成以下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为是否为“熟练盲拧者”与性别有关?
的把握认为是否为“熟练盲拧者”与性别有关?
熟练盲拧者 | 非熟练盲拧者 | |
男性 | ||
女性 |
(2)以这![]() 名盲拧魔方爱好者的用时不超过
名盲拧魔方爱好者的用时不超过![]() 秒的频率,代替全市所有盲拧魔方爱好者的用时不超过
秒的频率,代替全市所有盲拧魔方爱好者的用时不超过![]() 秒的概率,每位盲拧魔方爱好者用时是否超过
秒的概率,每位盲拧魔方爱好者用时是否超过![]() 秒相互独立.那么在该兴趣小组在全市范围内再次随机抽取
秒相互独立.那么在该兴趣小组在全市范围内再次随机抽取![]() 名爱好者进行测试,其中用时不超过
名爱好者进行测试,其中用时不超过![]() 秒的人数最有可能(即概率最大)是多少?
秒的人数最有可能(即概率最大)是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块半径为20米,圆心角![]() 的扇形展示台,展示台分成了四个区域:三角形
的扇形展示台,展示台分成了四个区域:三角形![]() ,弓形
,弓形![]() ,扇形
,扇形![]() 和扇形
和扇形![]() (其中
(其中![]() ).某次菊花展依次在这四个区域摆放:泥金香、紫龙卧雪、朱砂红霜、朱砂红霜.预计这三种菊花展示带来的日效益分别是:泥金香50元/米
).某次菊花展依次在这四个区域摆放:泥金香、紫龙卧雪、朱砂红霜、朱砂红霜.预计这三种菊花展示带来的日效益分别是:泥金香50元/米![]() ,紫龙卧雪30元/米
,紫龙卧雪30元/米![]() ,朱砂红霜40元/米
,朱砂红霜40元/米![]() .
.

(1)设![]() ,试建立日效益总量
,试建立日效益总量![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)试探求![]() 为何值时,日效益总量达到最大值.
为何值时,日效益总量达到最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在校园篮球赛中,甲、乙两个队10场比赛的得分数据整理成如图所示的茎叶图,下列说法正确的是( )
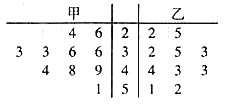
A.乙队得分的中位数是38.5
B.甲、乙两队得分在![]() 分数段频率相等
分数段频率相等
C.乙队的平均得分比甲队的高
D.甲队得分的稳定性比乙队好
查看答案和解析>>
科目:高中数学 来源: 题型:
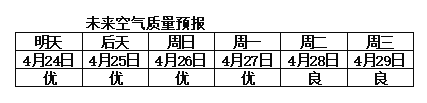
【题目】假设今天是4月23日,某市未来六天的空气质量预报情况如下图所示.该市有甲、乙、丙三人计划在未来六天(4月24日~4月29日)内选择一天出游,甲只选择空气质量为优的一天出游,乙不选择周一出游,丙不选择明天出游,且甲与乙不选择同一天出游,则这三人出游的不同方法数为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() ,
,![]() 是椭圆
是椭圆![]() 的左右顶点,点P是椭圆上的任意一点.
的左右顶点,点P是椭圆上的任意一点.
(1)证明:直线![]() ,与直线
,与直线![]() ,斜率之积为定值.
,斜率之积为定值.
(2)设经过![]() 且斜率不为0的直线
且斜率不为0的直线![]() 交椭圆于
交椭圆于![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年寒假是特殊的寒假,因为抗击疫情全体学生只能在家进行网上在线学习,为了研究学生在网上学习的情况,某学校在网上随机抽取120名学生对线上教育进行调查,其中男生与女生的人数之比为11∶13,其中男生30人对于线上教育满意,女生中有15名表示对线上教育不满意.
(1)完成![]() 列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
满意 | 不满意 | 总计 | |
男生 | 30 | ||
女生 | 15 | ||
合计 | 120 |
(2)从被调查的对线上教育满意的学生中,利用分层抽样抽取8名学生,再在8名学生中抽取3名学生,作线上学习的经验介绍,其中抽取男生的个数为![]() ,求出
,求出![]() 的分布列及期望值.
的分布列及期望值.
参考公式:附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 0.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com