判断函数f（x）＝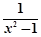
在区间（1，＋∞）上的单调性，并用单调性定义证明．
f（x）在区间（1，＋∞）上是减函数．利用定义证明
【解析】
试题分析：f（x）在区间（1，＋∞）上是减函数．证明如下： 2分
取任意的x1，x2∈（1，＋∞），且x1＜x2，则 3分
f（x1）－f（x2）＝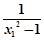
－
＝
＝
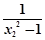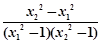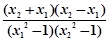． 5分
∵x1＜x2，∴x2－x1＞0． 6分
又∵x1，x2∈（1，＋∞），∴x2＋x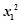1＞0，
－1＞0，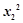
－1＞0， 8分
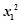∴（－1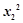）（－1）＞0．（x2＋x1）（x2－x1）＞0 10分
∴f（x1）－f（x2）＞0． 11分
根据定义知：f（x）在区间（1，＋∞）上是减函数． 12分
考点：本题考查了函数的单调性
点评：熟练掌握定义法证明函数的单调性的步骤是解决此类问题的关键，属基础题
科目：高中数学 来源： 题型：044
对于函数y＝f（x）（x∈D，D是此函数的定义域）若同时满足下列条件：
（Ⅰ）f（x）在D内单调递增或单调递减；
（Ⅱ）存在区间[a，b]
D，使f（x）在[a，b]上的值域为[a，b]；那么，把y＝f（x）（x∈D）叫闭函数．
（1）求闭函数y＝
符合条件（Ⅱ）的区间[a，b]；
（2）判断函数f（x）＝
（x∈
）是否为闭函数?并说明理由；
（3）若y＝
是闭函数，求实数k的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：044
已知a＞0，函数f（x）＝x3－ax
（1）当a＝2时，判断函数f（x）＝x3－ax在［1，＋∞］上单调性并加以证明；
（2）求a的取值范围，使f（x）＝x3－ax在［1，＋∞］上为增函数。
查看答案和解析>>
科目：高中数学 来源：数学教研室 题型：044
（1）当a＝2时，判断函数f（x）＝x3－ax在［1，＋∞］上单调性并加以证明；
（2）求a的取值范围，使f（x）＝x3－ax在［1，＋∞］上为增函数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com