
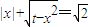 有相异实根的个数是( )
有相异实根的个数是( ) 等号两边均为正数,所以方程等价于两边平方得到的方程,再转化为t=2x2-2
等号两边均为正数,所以方程等价于两边平方得到的方程,再转化为t=2x2-2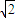 |x|+2,就可通过在同一坐标系中做出函数y=2x2-2
|x|+2,就可通过在同一坐标系中做出函数y=2x2-2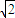 |x|+2,(-
|x|+2,(-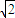 ≤x≤
≤x≤ )的图象和函数y=t,(1<t<2)的图象,通过判断图象交点个数来判断方程的相异实根根数.
)的图象和函数y=t,(1<t<2)的图象,通过判断图象交点个数来判断方程的相异实根根数.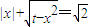 得,|x|≤
得,|x|≤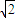 ,∴-
,∴- ≤x≤
≤x≤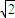
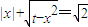 两边平方,得,t=2x2-2
两边平方,得,t=2x2-2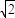 |x|+2
|x|+2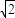 |x|+2 (-
|x|+2 (-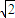 ≤x≤
≤x≤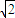 )的图象
)的图象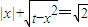 有相异实根的个数是4个.
有相异实根的个数是4个.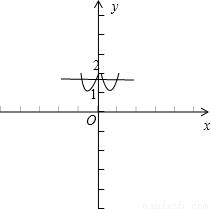


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
 设函数f(x)=
设函数f(x)=
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图放置的边长为1的正方形PABC沿x轴滚动(向右为顺时针,向左为逆时针).设顶点p(x,y)的轨迹方程是y=f(x),则关于f(x)的最小正周期T及y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积S的正确结论是( )
如图放置的边长为1的正方形PABC沿x轴滚动(向右为顺时针,向左为逆时针).设顶点p(x,y)的轨迹方程是y=f(x),则关于f(x)的最小正周期T及y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积S的正确结论是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com