
有 个小球,将它们任意分成两堆,求出这两堆小球球数的乘积,再将其中一堆小球任意分成两堆,求出这两堆小球球数的乘积,如此下去,每次都任选一堆,将这堆小球任意分成两堆,求出这两堆小球球数的乘积,直到不能再分为止,则所有乘积的和为 .
个小球,将它们任意分成两堆,求出这两堆小球球数的乘积,再将其中一堆小球任意分成两堆,求出这两堆小球球数的乘积,如此下去,每次都任选一堆,将这堆小球任意分成两堆,求出这两堆小球球数的乘积,直到不能再分为止,则所有乘积的和为 .
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:填空题
观察下面两个推理过程及结论:
(1) 若锐角A, B, C满足A+B+C= , 以角A, B, C分别为内角构造一个三角形, 依据正弦定理和余弦定理可得到等式:
, 以角A, B, C分别为内角构造一个三角形, 依据正弦定理和余弦定理可得到等式: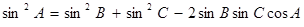
(2) 若锐角A, B, C满足A+B+C= , 则
, 则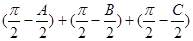 =
= , 以
, 以  分别为内角构造一个三角形, 依据正弦定理和余弦定理可以
分别为内角构造一个三角形, 依据正弦定理和余弦定理可以
得到的等式: 则:若锐角A, B, C满
则:若锐角A, B, C满
足A+B+C= , 类比上面推理方法, 可以得到一个等式是 .
, 类比上面推理方法, 可以得到一个等式是 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
半径为r的圆的面积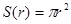 ,周长
,周长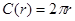 ,若将
,若将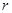 看作(0,+∞)上的变量,则
看作(0,+∞)上的变量,则 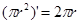 ① , ①式可用语言叙述为:圆的面积函数的导数等于圆的周长函数。
① , ①式可用语言叙述为:圆的面积函数的导数等于圆的周长函数。
对于半径为R的球,若将R看作(0,+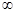 )上的变量,请你写出类似于①的式子:_______________________________________②
)上的变量,请你写出类似于①的式子:_______________________________________②
②式可用语言叙述为___________________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com