【答案】
分析:欲求
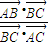
的值,由于
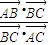
=
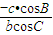
,故须求出三角形的内角及边的比值,设出三角形的三边分别为a,b,c,根据由G为三角形的重心,根据中线的性质及向量的加法法则分别表示出
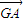
,
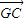
和
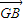
,代入化简后的式子中,然后又根据
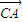
等于

加
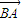
,把上式进行化简,最后得到关于
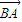
和
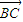
的关系式,由
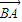
和
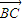
为非零向量,得到两向量前的系数等于0,列出关于a,b及c的方程组,不妨令b=

,,即可求出a与b的值,然后根据余弦定理表示出cosB,把a,b,c的值代入即可求出cosB的值,同理求得cosC即得.
解答:解:因为
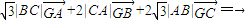
设三角形的边长顺次为a,b,c,根据正弦定理得:
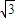
a
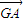
+2b
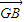
+2
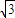
c
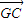
=

,
由点G为三角形的重心,根据中线的性质及向量加法法则得:
3

=
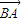
+
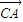
,3
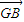
=
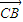
+
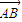
,3
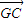
=
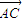
+
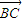
,
代入上式得:
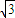
a(
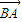
+
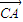
)+2b(
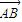
+
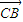
)+2
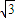
c(
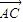
+
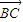
)=
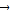
,
又
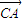
=
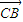
+
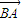
,上式可化为:
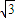
a(2
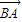
+
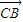
)+2b(
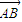
+
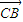
)+2

c(-

+2
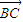
)=
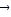
,
即(2

a-2b-2
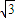
c)
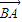
+(-
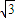
a-2b+4
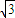
c)
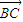
=

,
则有
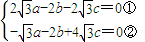
,令b=
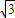
,解得:
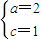
,
所以cosB=
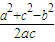
=
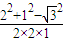
=

,
cosC=
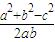
=
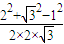
=
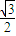
,
∴
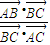
=
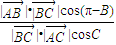
=
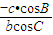
=
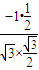
=-

故答案为:
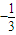 点评:
点评:此题考查学生灵活运用向量在几何中的应用、余弦定理化简求值,掌握向量的加法法则及中线的性质,是一道中档题.

 ,则
,则 的值= .
的值= . 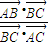 的值,由于
的值,由于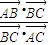 =
=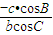 ,故须求出三角形的内角及边的比值,设出三角形的三边分别为a,b,c,根据由G为三角形的重心,根据中线的性质及向量的加法法则分别表示出
,故须求出三角形的内角及边的比值,设出三角形的三边分别为a,b,c,根据由G为三角形的重心,根据中线的性质及向量的加法法则分别表示出 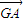 ,
,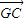 和
和 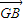 ,代入化简后的式子中,然后又根据
,代入化简后的式子中,然后又根据 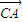 等于
等于  加
加 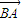 ,把上式进行化简,最后得到关于
,把上式进行化简,最后得到关于 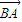 和
和 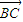 的关系式,由
的关系式,由 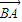 和
和 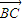 为非零向量,得到两向量前的系数等于0,列出关于a,b及c的方程组,不妨令b=
为非零向量,得到两向量前的系数等于0,列出关于a,b及c的方程组,不妨令b= ,,即可求出a与b的值,然后根据余弦定理表示出cosB,把a,b,c的值代入即可求出cosB的值,同理求得cosC即得.
,,即可求出a与b的值,然后根据余弦定理表示出cosB,把a,b,c的值代入即可求出cosB的值,同理求得cosC即得.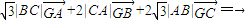
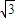 a
a 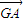 +2b
+2b 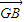 +2
+2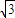 c
c 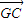 =
= ,
, =
=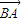 +
+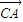 ,3
,3 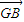 =
=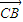 +
+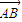 ,3
,3 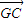 =
=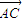 +
+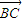 ,
,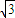 a(
a( 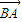 +
+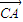 )+2b(
)+2b( 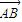 +
+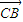 )+2
)+2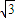 c(
c( 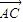 +
+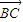 )=
)=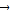 ,
,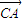 =
=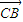 +
+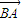 ,上式可化为:
,上式可化为: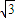 a(2
a(2 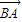 +
+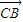 )+2b(
)+2b( 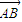 +
+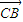 )+2
)+2 c(-
c(- +2
+2 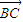 )=
)=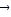 ,
, a-2b-2
a-2b-2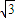 c)
c) 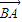 +(-
+(-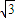 a-2b+4
a-2b+4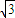 c)
c) 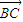 =
= ,
,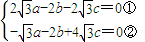 ,令b=
,令b=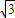 ,解得:
,解得: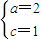 ,
,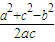 =
=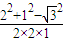 =
= ,
,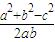 =
=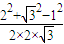 =
=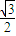 ,
,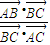 =
=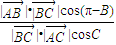 =
=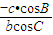 =
=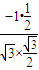 =-
=-
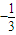


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案