
【题目】已知函数![]() 在x = 2处的切线与直线
在x = 2处的切线与直线![]() 垂直.
垂直.
(Ⅰ)求函数f (x)的单调区间;
(Ⅱ)若存在![]() ,使
,使![]() 成立,求m的最小值.
成立,求m的最小值.
【答案】(Ⅰ)函数f (x)的单调递减区间是(0,1],单调递增区间是[1,+∞);(Ⅱ)m的最小值是5.
【解析】试题分析:1)求出函数的导数,根据f′(2)的值,求出a,从而求出函数的单调区间;
(2)问题等价于当x∈(1,+∞)时,![]() 成立,设
成立,设![]() ,根据函数的单调性判断即可.
,根据函数的单调性判断即可.
试题解析:
(Ⅰ)![]()
由已知,![]() ,解得:a = 1
,解得:a = 1
∴![]()
当![]() 时,
时,![]() ,f (x)是减函数
,f (x)是减函数
当![]() 时,
时,![]() ,f (x)是增函数
,f (x)是增函数
∴函数f (x)的单调递减区间是(0,1],单调递增区间是[1,+∞).
(Ⅱ)解:∵![]() ,∴
,∴![]() 等价于
等价于![]()
即存在![]() ,使
,使![]() 成立,∴
成立,∴![]()
设![]() ,则
,则![]()
设![]() ,则
,则![]()
∴h (x)在![]() 上单调递增.
上单调递增.
又h (3) < 0,h (4) > 0,∴h (x)在![]() 上有唯一零点,设为x0,则
上有唯一零点,设为x0,则![]() ,且
,且![]()
![]()
又![]() ,∴m的最小值是5.
,∴m的最小值是5.


科目:高中数学 来源: 题型:
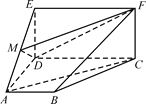
【题目】如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,![]() ,M是线段AE上的动点.
,M是线段AE上的动点.
(1)试确定点M的位置,使AC∥平面DMF,并说明理由;
(2)在(1)的条件下,求平面DMF与平面ABCD所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现从中随机抽取100人的数学与地理的水平测试成绩如下表:
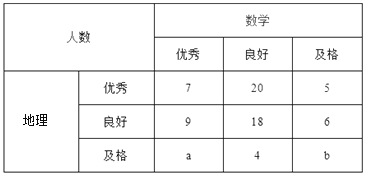
成绩分为优秀、良好、及格三个等级;横向,纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有![]() .
.
(Ⅰ)若在该样本中,数学成绩优秀率是30%,求![]() 的值;
的值;
(Ⅱ)已知![]() ,求数学成绩为优秀的人数比及格的人数少的概率.
,求数学成绩为优秀的人数比及格的人数少的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 定义在
定义在![]() 上的奇函数,
上的奇函数, ![]() 的最大值为
的最大值为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)关于![]() 的方程
的方程![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3)若存在![]() ,不等式
,不等式![]() 成立,请同学们探究实数
成立,请同学们探究实数![]() 的所有可能取值.
的所有可能取值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第![]() 届夏季奥林匹克运动会将于 2016 年 8 月 5 日—21 日在巴西里约热内卢举行.下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据( 单位: 枚).
届夏季奥林匹克运动会将于 2016 年 8 月 5 日—21 日在巴西里约热内卢举行.下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据( 单位: 枚).
第 | 第 | 第 | 第 | 第 | |
中国 |
|
|
|
|
|
俄罗斯 |
|
|
|
|
|
(1)根据表格中两组数据完成近五届奥运会两国代表团获得的金牌数的茎叶图, 并通过茎叶图比较两国代表团获得的金牌数的平均值及分散程度( 不要求计算出具体数值, 给出结论即可);
(2)甲、 乙、 丙三人竞猜今年中国代表团和俄罗斯代表团中的哪一个获得的金牌数多( 假设两国代表团获得的金牌数不会相等) , 规定甲、 乙、 丙必须在两个代表团中选一个, 已知甲、 乙猜中国代表团的概率都为![]() , 丙猜中国代表团的概率为
, 丙猜中国代表团的概率为![]() , 三人各自猜哪个代表团的结果互不影响.现让甲、 乙、 丙各猜一次, 设三人中猜中国代表团的人数为
, 三人各自猜哪个代表团的结果互不影响.现让甲、 乙、 丙各猜一次, 设三人中猜中国代表团的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用另一种方法表示下列集合.
(1){x||x|≤2,x∈Z};
(2){能被3整除,且小于10的正数};
(3)坐标平面内在第四象限的点组成的集合.
(4){(x,y)|x+y=6,x,y均为正整数};
(5){-3,-1,1,3,5}.
(6)被3除余2的正整数集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,且x≤0时,f(x)=log![]() (-x+1).
(-x+1).
(1)求f(0),f(1);
(2)求函数f(x)的解析式;
(3)若f(a-1)<-1,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com