
分析 (1)设点P(x,y),由题意可得:$\frac{|PF|}{|y+2|}$=$\frac{\sqrt{{x}^{2}+(y+1)^{2}}}{|y+2|}$=$\frac{\sqrt{2}}{2}$,化简即可得出.
(2)E(0,$\frac{1}{2}$).分类讨论:①r≥$\sqrt{2}$+$\frac{1}{2}$,根据|MN|≥0.5,可得r≥$\sqrt{2}$+$\frac{1}{2}$+$\frac{1}{2}$.②0<r<$\sqrt{2}$+$\frac{1}{2}$,设M$(cosθ,\sqrt{2}sinθ)$,|MN|=|EM|-r$≥\frac{1}{2}$,解得r≤|EM|-$\frac{1}{2}$的最小值,即可得出r的取值范围.
(3)把x=-$\frac{1}{3}$代入椭圆的方程可得:$\frac{1}{9}$+$\frac{{y}^{2}}{2}$=1,解得y=±$\frac{4}{3}$.取点T(1,0)时满足$\overrightarrow{TA}•\overrightarrow{TB}$=0.下面证明:在此坐标平面上存在一个定点T(1,0),使得无论l如何转动,以AB为直径的圆恒过点T(1,0).设过点Q(-$\frac{1}{3}$,0)的动直线l的方程为:y=k(x+$\frac{1}{3}$),A(x1,y1),B(x2,y2).与椭圆方程化为:(18+9k2)x2+6k2x+k2-18=0,利用根与系数的关系、数量积运算性质可得$\overrightarrow{TA}•\overrightarrow{TB}$=(x1-1)(x2-1)+${k}^{2}({x}_{1}+\frac{1}{3})$$({x}_{2}+\frac{1}{3})$=0.即可证明.
解答 解:(1)设点P(x,y),由题意可得:$\frac{|PF|}{|y+2|}$=$\frac{\sqrt{{x}^{2}+(y+1)^{2}}}{|y+2|}$=$\frac{\sqrt{2}}{2}$,化为:x2+$\frac{{y}^{2}}{2}$=1.
(2)E(0,$\frac{1}{2}$).
分类讨论:①r≥$\sqrt{2}$+$\frac{1}{2}$,∵总有|MN|≥0.5,∴r≥$\sqrt{2}$+$\frac{1}{2}$+$\frac{1}{2}$=$\sqrt{2}$+1.
②0<r<$\sqrt{2}$+$\frac{1}{2}$,设M$(cosθ,\sqrt{2}sinθ)$,
|MN|=|EM|-r$≥\frac{1}{2}$,解得r≤|EM|-$\frac{1}{2}$=$\sqrt{co{s}^{2}θ+(\sqrt{2}sinθ-\frac{1}{2})^{2}}$-$\frac{1}{2}$=$\sqrt{(sinθ-\frac{\sqrt{2}}{2})^{2}+\frac{3}{4}}$-$\frac{1}{2}$,
∴$0<r≤\frac{\sqrt{3}-1}{2}$.
综上可得:r的取值范围是$(0,\frac{\sqrt{3}-1}{2}]$∪$[\sqrt{2}+1,+∞)$.
(3)把x=-$\frac{1}{3}$代入椭圆的方程可得:$\frac{1}{9}$+$\frac{{y}^{2}}{2}$=1,解得y=±$\frac{4}{3}$.取A$(-\frac{1}{3},\frac{4}{3})$,B$(-\frac{1}{3},-\frac{4}{3})$.
取点T(1,0)时满足$\overrightarrow{TA}•\overrightarrow{TB}$=0.
下面证明:在此坐标平面上存在一个定点T(1,0),使得无论l如何转动,以AB为直径的圆恒过点T.
设过点Q(-$\frac{1}{3}$,0)的动直线l的方程为:y=k(x+$\frac{1}{3}$),A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{y=k(x+\frac{1}{3})}\\{{x}^{2}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,化为:(18+9k2)x2+6k2x+k2-18=0,
∴x1+x2=$-\frac{6{k}^{2}}{18+9{k}^{2}}$,x1x2=$\frac{{k}^{2}-18}{18+9{k}^{2}}$.
则$\overrightarrow{TA}•\overrightarrow{TB}$=(x1-1)(x2-1)+y1y2=(x1-1)(x2-1)+${k}^{2}({x}_{1}+\frac{1}{3})$$({x}_{2}+\frac{1}{3})$=(1+k2)x1x2+$(\frac{1}{3}{k}^{2}-1)$(x1+x2)+1+$\frac{1}{9}{k}^{2}$=(1+k2)×$\frac{{k}^{2}-18}{18+9{k}^{2}}$-$(\frac{1}{3}{k}^{2}-1)$×$\frac{6{k}^{2}}{18+9{k}^{2}}$+1+$\frac{1}{9}{k}^{2}$=0.
∴在此坐标平面上存在一个定点T(1,0),使得无论l如何转动,以AB为直径的圆恒过点T.
点评 本题考查了椭圆的标准方程、直线与椭圆相交转化为一元二次方程的根与系数的关系、点与圆的位置关系、圆的性质、数量积运算性质,考查了分类讨论方法、推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
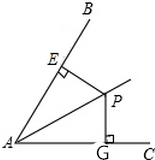 如图,点P是∠BAC内一点,且P到AB、AC的距离PE=PG,则下列哪一个能作为△PEA≌△PGA的理由( )
如图,点P是∠BAC内一点,且P到AB、AC的距离PE=PG,则下列哪一个能作为△PEA≌△PGA的理由( )| A. | HL | B. | AAS | C. | SSS | D. | ASA |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com