【答案】
分析:(1)由P(a
n,a
n+1)在函数f(x)=x+2图象上,得到数列{a
n}是等差数列,直接由等差数列的通项公式求数列a
n;再利用2,b
n,S
n成等差数列得到数列{b
n}的递推式,首先求出b
1,由递推式可以判定数列{b
n}是等比数列,由等比数列的通项公式写出b
n;
(2)把数列{a
n},{b
n}的通项公式代入
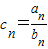
,然后利用错位相减法求出数列{c
n}的前n项和
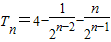
由此可以得到存在最小的正整数4,使对任意 n∈N
*都有T
n<4.
解答:解:(1)∵点(a
n,a
n+1)在f(x)=x+2的图象上,
∴a
n+1=a
n+2,
∴a
n+1-a
n=2,
∴{a
n}是以2为公差的等差数列,
又a
1=2,
则a
n=a
1+(n-1)d=2+2(n-1)=2n.
由2,b
n,S
n成等差数列,
所以S
n+2=2b
n ①
当n=1时,b
1+2=2b
1,所以b
1=2.
当n≥2时,S
n-1+2=2b
n-1②
①-②得:b
n=2b
n-2b
n-1.
所以b
n=2b
n-1(n≥2).
因为b
1=2≠0,所以
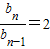
(n≥2).
故数列{b
n}是以2为首项,以2为公比的等比数列.
所以
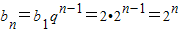
;
(2)由
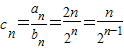
.
所以{c
n}的前n项和
T
n=c
1+c
2+…+c
n=
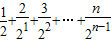
③
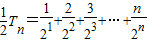
④
③-④得:
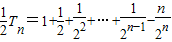
=
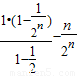
.
所以
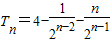
<4.
所以存在最小的正整数m=4,使对任意 n∈N
*都有T
n<4.
点评:本题是等差数列和等比数列的综合题,考查了等差数列和等比数列的确定,考查了等差数列和等比数列的通项公式,关键是对n=1和n≥2进行讨论,考查了利用错位相减法求数列的和,是中档题.

 .问是否存在最小的正整数m,使对任意 n∈N*都有Tn<m.若存在,求出m的值,否则,说明理由.
.问是否存在最小的正整数m,使对任意 n∈N*都有Tn<m.若存在,求出m的值,否则,说明理由.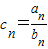 ,然后利用错位相减法求出数列{cn}的前n项和
,然后利用错位相减法求出数列{cn}的前n项和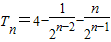
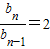 (n≥2).
(n≥2).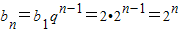 ;
;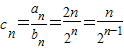 .
.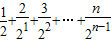 ③
③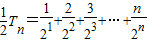 ④
④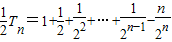
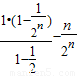 .
.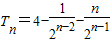 <4.
<4.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案