
| x2-x+n |
| x2+1 |
| a | n |
| 1 |
| 2 |
| Sn |
| n+c |
| dn |
| (n+36)dn+1 |
| x2-x+n |
| x2+1 |
|
| 2n2-n |
| n+c |
| 1 |
| 1+c |
| 6 |
| 2+c |
| 15 |
| 3+c |
| 1 |
| 2 |
| 1 |
| 2 |
| 2n |
| (n+36)(2n+2) |
| 1 | ||
n+
|
| 1 | ||
37+2
|
| 1 |
| 49 |
|


科目:高中数学 来源: 题型:
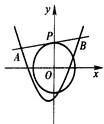 设点P(m,n)在圆x2+y2=2上,l是过点P的圆的切线,切线l与函数y=x2+x+k(k∈R)的图象交于A,B两点,点O是坐标原点.
设点P(m,n)在圆x2+y2=2上,l是过点P的圆的切线,切线l与函数y=x2+x+k(k∈R)的图象交于A,B两点,点O是坐标原点.查看答案和解析>>
科目:高中数学 来源: 题型:
| MN |
| MA |
| MB |
| MN |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求g2(x),g3(x)的表达式,并猜想gn(x)(n∈N*)的表达式(直接写出猜想结果);
(2)若关于x的函数y=x2+![]() (x)(n∈N*)在区间(-∞,-1]上的最小值为6,求n的值.(符号“
(x)(n∈N*)在区间(-∞,-1]上的最小值为6,求n的值.(符号“![]() ”表示求和,例如:
”表示求和,例如:![]() =1+2+3+…+n).
=1+2+3+…+n).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com