
分析 (Ⅰ)求出函数的导数,求得切线的斜率,由两直线平行的条件可得a值;
(Ⅱ)求出函数的导函数,然后对a分类分析得答案;
(Ⅲ)构造函数g(x)=f(x)-(e-1)x=ex-ax-ex+x,利用导数求其最小值,由最小值恒大于0得答案.
解答 (Ⅰ)解:f(x)=ex-ax的导数为f′(x)=ex-a,
曲线y=f(x)在x=1处的切线斜率为k=e-a,
由切线与直线y=ax+2平行,
得e-a=a,解得a=$\frac{e}{2}$.
(Ⅱ)解:f′(x)=ex-a,
若a≤0,则f′(x)>0,则f(x)在(-∞,+∞)上为增函数;
若a>0,则当x>lna时,f′(x)>0,f(x)在(lna,+∞)上递增;
当x<lna时,f′(x)<0,f(x)在(-∞,lna)上递减.
(Ⅲ)证明:令g(x)=f(x)-(e-1)x=ex-ax-ex+x,
则g′(x)=ex-a-e+1,
由g′(x)=ex-a-e+1=0,得x=ln(a+e-1).
∴当x>ln(a+e-1)时,f′(x)>0,f(x)在(ln(a+e-1),+∞)上递增;
当x<ln(a+e-1)时,f′(x)<0,f(x)在(-∞,ln(a+e-1))上递减.
∴g(x)在(-∞,+∞)上有极小值也就是最小值为g(ln(a+e-1))=eln(a+e-1)-(a+e-1)ln(a+e-1)
=(a+e-1)(1-ln(a+e-1)).
∵0<a<1,∴0<a+e-1<e,
则ln(a+e-1)<1,
∴g(ln(a+e-1))=(a+e-1)(1-ln(a+e-1))>0.
∴曲线y=f(x)在直线y=(e-1)x的上方.
点评 本题考查利用导数研究函数的单调性,考查利用导数求函数的最值,考查数学转化思想方法,是中档题.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $({\frac{4}{5},\frac{3}{5}})$或$({-\frac{4}{5},\frac{3}{5}})$ | B. | $({\frac{3}{5},-\frac{4}{5}})$或$({-\frac{3}{5},\frac{4}{5}})$ | C. | $({-\frac{4}{5},-\frac{3}{5}})$或$({\frac{4}{5},\frac{3}{5}})$ | D. | $({-\frac{3}{5},-\frac{4}{5}})$或$({\frac{3}{5},\frac{4}{5}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$-$\frac{4}{5}$i | B. | $\frac{3}{5}$+$\frac{4}{5}$i | C. | $\frac{4}{5}$+$\frac{3}{5}$i | D. | $\frac{4}{5}$-$\frac{3}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
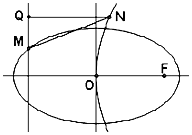 椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上有一点M(-4,$\frac{9}{5}$)在抛物线y2=2px(p>0)的准线l上,抛物线的焦点也是椭圆焦点.
椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上有一点M(-4,$\frac{9}{5}$)在抛物线y2=2px(p>0)的准线l上,抛物线的焦点也是椭圆焦点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com