
 为了了解高中生的身体健康情况,体育局随机抽取了某校20名学生的体育测试成绩,得到如图所示的茎叶图:
为了了解高中生的身体健康情况,体育局随机抽取了某校20名学生的体育测试成绩,得到如图所示的茎叶图:分析 (1)由茎叶图知“优秀成绩”人数为4人,从这20人中随机选取3人,设选中优秀人数为X,用事件A表示“从这20人中随机选取3人,至多有1人是‘优秀成绩’”,则P(A)=P(X=0)+P(X=1),由此能求出从这20人中随机选取3人,至多有1人是“优秀成绩”的概率.
(2)由样本估计总体,可知抽到“优秀成绩”学生的概率p=$\frac{1}{5}$,ξ的可能取值为0,1,2,3,且ξ~B(3,$\frac{1}{5}$),由此能求出ξ的分布列及数学期望、方差.
解答 解:(1)由茎叶图知“优秀成绩”人数为4人,
从这20人中随机选取3人,设选中优秀人数为X,
用事件A表示“从这20人中随机选取3人,至多有1人是‘优秀成绩’”,
则P(A)=P(X=0)+P(X=1)
=$\frac{{C}_{18}^{3}}{{C}_{20}^{3}}+\frac{{C}_{18}^{2}{C}_{4}^{1}}{{C}_{20}^{3}}$=$\frac{52}{57}$.
(2)由样本估计总体,可知抽到“优秀成绩”学生的概率p=$\frac{1}{5}$,
ξ的可能取值为0,1,2,3,且ξ~B(3,$\frac{1}{5}$),
P(ξ=0)=${C}_{3}^{0}(\frac{4}{5})^{3}$=$\frac{64}{125}$,
P(ξ=1)=${C}_{3}^{1}(\frac{4}{5})^{2}(\frac{1}{5})$=$\frac{48}{125}$,
P(ξ=2)=${C}_{3}^{2}(\frac{4}{5})(\frac{1}{5})^{2}$=$\frac{12}{125}$,
P(ξ=3)=${C}_{3}^{3}(\frac{1}{5})^{3}$=$\frac{1}{125}$,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{64}{125}$ | $\frac{48}{125}$ | $\frac{12}{125}$ | $\frac{1}{125}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列、数学期望和方差的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
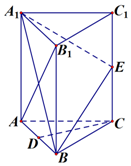 如图,在正三棱柱ABC-A1B1C1中,每条棱长均相等,D为棱AB的中点,E为侧棱CC1的中点.
如图,在正三棱柱ABC-A1B1C1中,每条棱长均相等,D为棱AB的中点,E为侧棱CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{5}{2},-2)$ | B. | $(-∞,-\frac{5}{2}]$ | C. | (-∞,-2] | D. | $[-\frac{5}{2},-2]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | h(x)=f(x)+g(x)是偶函数 | B. | h(x)=f(x)+g(x)是奇函数 | ||
| C. | h(x)=f(x)g(x)是奇函数 | D. | h(x)=f(x)g(x)是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | -$\frac{2\sqrt{2}}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $±\frac{2\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 条件 | 方程 |
| ①△ABC周长为10 | C1:y2=25 |
| ②△ABC面积为10 | C2:x2+y2=4(y≠0) |
| ③△ABC中,∠A=90° | C3:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1(y≠0) |
| A. | C3,C1,C2 | B. | C1,C2,C3 | C. | C3,C2,C1 | D. | C1,C3,C2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com