
【题目】如图,在棱长为2的正方体ABCDA1B1C1D1中,P为棱C1D1的中点,Q为棱BB1上的点,且BQ=λBB1(λ≠0).
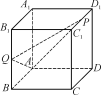
(1)若λ=![]() ,求AP与AQ所成角的余弦值;
,求AP与AQ所成角的余弦值;
(2)若直线AA1与平面APQ所成的角为45°,求实数λ的值.
【答案】(1)![]() .(2)λ=
.(2)λ=![]() .
.
【解析】
(1)先根据题意建立空间直角坐标系,求得向量![]() 和向量
和向量![]() 的坐标,再利用线线角的向量方法求解.
的坐标,再利用线线角的向量方法求解.
(2)由BQ=λBB1,表示![]() =(2,0,2λ) ,从而得到平面APQ的一个法向量
=(2,0,2λ) ,从而得到平面APQ的一个法向量![]() =(2λ,2-λ,-2),再根据直线AA1与平面APQ所成角为45°,由|cos〈
=(2λ,2-λ,-2),再根据直线AA1与平面APQ所成角为45°,由|cos〈![]() ,
,![]() 〉|=
〉|=![]() =
=![]() =
=![]() 求解.
求解.
(1)以![]() 为正交基底,建立如图所示空间直角坐标系Axyz.
为正交基底,建立如图所示空间直角坐标系Axyz.
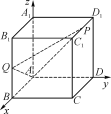
因为![]() =(1,2,2),
=(1,2,2),![]() =(2,0,1),
=(2,0,1),
所以cos〈![]() ,
,![]() 〉=
〉=![]() =
=![]() =
=![]() .
.
所以AP与AQ所成角的余弦值为![]() .
.
(2) 由题意可知,![]() =(0,0,2),
=(0,0,2),![]() =(2,0,2λ).
=(2,0,2λ).
设平面APQ的法向量为![]() =(x,y,z),
=(x,y,z),
则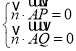 即
即![]()
令z=-2,则x=2λ,y=2-λ.
所以![]() =(2λ,2-λ,-2).
=(2λ,2-λ,-2).
又因为直线AA1与平面APQ所成角为45°,
所以|cos〈![]() ,
,![]() 〉|=
〉|=![]()
=![]() =
=![]() ,
,
可得5λ2-4λ=0,
又因为λ≠0,所以λ=![]()


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,![]() 是正方形,点
是正方形,点![]() 在以
在以![]() 为直径的半圆弧上(
为直径的半圆弧上(![]() 不与
不与![]() ,
,![]() 重合),
重合),![]() 为线段
为线段![]() 的中点,现将正方形
的中点,现将正方形![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.
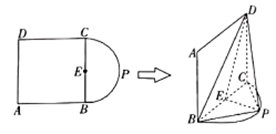
(1)证明:![]() 平面
平面![]() .
.
(2)若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,求
的体积最大时,求![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,PA⊥底面ABCD,AD∥BC,AB=AC=AD=3,PA=BC=4.
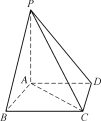
(1)求异面直线PB与CD所成角的余弦值;
(2)求平面PAD与平面PBC所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,A1A=AB=2,∠ABC=![]() ,E,F分别是BC,A1C的中点.
,E,F分别是BC,A1C的中点.
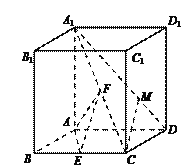
(1)求异面直线EF,AD所成角的余弦值;
(2)点M在线段A1D上, ![]() .若CM∥平面AEF,求实数λ的值.
.若CM∥平面AEF,求实数λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 与
与![]() 满足
满足![]() ,
,![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和(
项和(![]() ).
).
(1)设数列![]() 是首项和公比都为
是首项和公比都为![]() 的等比数列,且数列
的等比数列,且数列![]() 也是等比数列,求
也是等比数列,求![]() 的值;
的值;
(2)设![]() ,若
,若![]() 且
且![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)设![]() ,
,![]() ,
,![]() (
(![]() ,
,![]() ),若存在整数
),若存在整数![]() ,
,![]() ,且
,且![]() ,使得
,使得![]() 成立,求
成立,求![]() 的所有可能值.
的所有可能值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型,在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃,让一个小球从高尔顿板上方的通道口落下,小球在下落的过程中与层层小木块碰撞,且等可能向左或向右滚下,最后掉入高尔顿板下方的某一球槽内.如图所示的小木块中,上面7层为高尔顿板,最下面一层为改造的高尔顿板,小球从通道口落下,第一次与第2层中间的小木块碰撞,以![]() 的概率向左或向右滚下,依次经过6次与小木块碰撞,最后掉入编号为1,2…,7的球槽内.例如小球要掉入3号球槽,则在前5次碰撞中有2次向右3次向左滚到第6层的第3个空隙处,再以
的概率向左或向右滚下,依次经过6次与小木块碰撞,最后掉入编号为1,2…,7的球槽内.例如小球要掉入3号球槽,则在前5次碰撞中有2次向右3次向左滚到第6层的第3个空隙处,再以![]() 的概率向左滚下,或在前5次碰撞中有1次向右4次向左滚到第6层的第2个空隙处,再以
的概率向左滚下,或在前5次碰撞中有1次向右4次向左滚到第6层的第2个空隙处,再以![]() 的概率向右滚下.
的概率向右滚下.

(1)若进行一次高尔顿板试验,求小球落入第7层第6个空隙处的概率;
(2)小明同学在研究了高尔顿板后,利用该图中的高尔顿板来到社团文化节上进行盈利性“抽奖”活动,8元可以玩一次高尔顿板游戏,小球掉入X号球槽得到的奖金为![]() 元,其中
元,其中![]() .
.
(i)求X的分布列:
(ii)高尔顿板游戏火爆进行,很多同学参加了游戏,你觉得小明同学能盈利吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国庆70周年庆典磅礴而又欢快的场景,仍历历在目.已知庆典中某省的游行花车需要用到某类花卉,而该类花卉有甲、乙两个品种,花车的设计团队对这两个品种进行了检测.现从两个品种中各抽测了10株的高度,得到如下茎叶图.下列描述正确的是( )

A.甲品种的平均高度大于乙品种的平均高度,且甲品种比乙品种长的整齐
B.甲品种的平均高度大于乙品种的平均高度,但乙品种比甲品种长的整齐
C.乙品种的平均高度大于甲品种的平均高度,且乙品种比甲品种长的整齐
D.乙品种的平均高度大于甲品种的平均高度,但甲品种比乙品种长的整齐
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com