
【题目】如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,A1A=AB=2,∠ABC=![]() ,E,F分别是BC,A1C的中点.
,E,F分别是BC,A1C的中点.
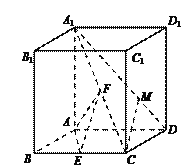
(1)求异面直线EF,AD所成角的余弦值;
(2)点M在线段A1D上, ![]() .若CM∥平面AEF,求实数λ的值.
.若CM∥平面AEF,求实数λ的值.
【答案】(1) ![]() .(2)
.(2)![]() .
.
【解析】试题分析:(1)由四棱柱![]() ,证得
,证得![]() ,进而得到
,进而得到![]() ,以
,以![]() 为正交基底建立空间直角坐标系,利用向量坐标运算,即可求解
为正交基底建立空间直角坐标系,利用向量坐标运算,即可求解![]() 所成角的余弦值;
所成角的余弦值;
(2)设![]() ,由点
,由点![]() 在线段
在线段![]() 上,得到
上,得到![]() ,得出向量
,得出向量![]() 则坐标表示,再求得平面
则坐标表示,再求得平面![]() 的一个法向量,利用向量的数量积的运算,即可得到
的一个法向量,利用向量的数量积的运算,即可得到![]() 的值。
的值。
试题解析:
因为四棱柱ABCD-A1B1C1D1为直四棱柱,所以A1A⊥平面ABCD.
又AE平面ABCD,AD平面ABCD,所以A1A⊥AE,A1A⊥AD.

在菱形ABCD中∠ABC=![]() ,则△ABC是等边三角形.
,则△ABC是等边三角形.
因为E是BC中点,所以BC⊥AE.
因为BC∥AD,所以AE⊥AD.
以{![]() ,
,![]() ,
,![]() }为正交基底建立空间直角坐标系.
}为正交基底建立空间直角坐标系.
则A(0,0,0),C(![]() ,1,0),D(0,2,0),
,1,0),D(0,2,0),
A1(0,0,2),E(![]() ,0,0),F(
,0,0),F(![]() ,,1).
,,1).
(1)![]() =(0,2,0),
=(0,2,0),![]() =(-
=(-![]() ,,1),所以
,,1),所以![]() ·
·![]() =1.
=1.
从而cos<![]() ,
,![]() >=
>=![]() =
=![]() .
.
故异面直线EF,AD所成角的余弦值为![]() .
.
(2)设M(x,y,z),由于点M在线段A1D上,且![]() =λ,
=λ,
则![]() =λ
=λ![]() ,即(x,y,z-2)=λ(0,2,-2).
,即(x,y,z-2)=λ(0,2,-2).
则M(0,2λ,2-2λ),![]() =(-
=(-![]() ,2λ-1,2-2λ).
,2λ-1,2-2λ).
设平面AEF的法向量为n=(x0,y0,z0).
因为![]() =(
=(![]() ,0,0),
,0,0),![]() =(
=(![]() ,,1),
,,1),
由n·![]() =0,n·
=0,n·![]() =0,得x0=0, y0+z0=0.
=0,得x0=0, y0+z0=0.
取y0=2,则z0=-1,
则平面AEF的一个法向量为n=(0,2,-1).
由于CM∥平面AEF,则n·![]() =0,即2(2λ-1)-(2-2λ)=0,解得λ=.
=0,即2(2λ-1)-(2-2λ)=0,解得λ=.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的左焦点
)的左焦点![]() 与抛物线
与抛物线![]() 的焦点重合,直线
的焦点重合,直线![]() 与以原点
与以原点![]() 为圆心,以椭圆的离心率
为圆心,以椭圆的离心率![]() 为半径的圆相切.
为半径的圆相切.
(Ⅰ)求该椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线交椭圆于
的直线交椭圆于![]() ,
, ![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,
, ![]() 的垂直平分线与
的垂直平分线与![]() 轴和
轴和![]() 轴分别交于
轴分别交于![]() ,
, ![]() 两点.记
两点.记![]() 的面积为
的面积为![]() ,
, ![]() 的面积为
的面积为![]() .问:是否存在直线
.问:是否存在直线![]() ,使得
,使得![]() ,若存在,求直线
,若存在,求直线![]() 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为I的函数y=f(x),如果存在区间[m,n]I,同时满足:
①f(x)在[m,n]内是单调函数;
②当定义域是[m,n],f(x)值域也是[m,n],则称[m,n]是函数y=f(x)的“好区间”.
(1)设g(x)=loga(ax﹣2a)+loga(ax﹣3a)(其中a>0且a≠1),求g(x)的定义域并判断其单调性;
(2)试判断(1)中的g(x)是否存在“好区间”,并说明理由;
(3)已知函数P(x)= ![]() (t∈R,t≠0)有“好区间”[m,n],当t变化时,求n﹣m 的最大值.
(t∈R,t≠0)有“好区间”[m,n],当t变化时,求n﹣m 的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小张在淘宝网上开一家商店,他以10元每条的价格购进某品牌积压围巾2000条.定价前,小张先搜索了淘宝网上的其它网店,发现:A商店以30元每条的价格销售,平均每日销售量为10条;B商店以25元每条的价格销售,平均每日销售量为20条.假定这种围巾的销售量t(条)是售价x(元)(x∈Z+)的一次函数,且各个商店间的售价、销售量等方面不会互相影响.
(1)试写出围巾销售每日的毛利润y(元)关于售价x(元)(x∈Z+)的函数关系式(不必写出定义域),并帮助小张定价,使得每日的毛利润最高(每日的毛利润为每日卖出商品的进货价与销售价之间的差价);
(2)考虑到这批围巾的管理、仓储等费用为200元/天(只要围巾没有售完,均须支付200元/天,管理、仓储等费用与围巾数量无关),试问小张应该如何定价,使这批围巾的总利润最高(总利润=总毛利润﹣总管理、仓储等费用)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在区间[0,a]上的函数f(x)的图象如图所示,记以A(0,f(0)),B(a,f(a)),C(x,f(x))为顶点的三角形的面积为S(x),则函数S(x)的导函数S′(x)的图象大致是( ) 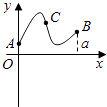
A.
B.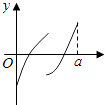
C.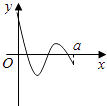
D.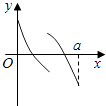
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有![]() (n≥2,n∈N*)个给定的不同的数随机排成一个下图所示的三角形数阵:
(n≥2,n∈N*)个给定的不同的数随机排成一个下图所示的三角形数阵:

设Mk是第k行中的最大数,其中1≤k≤n,k∈N*.记M1<M2<…<Mn的概率为pn.
(1)求p2的值;
(2)证明:pn>![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,然后在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒(如图).设小正方形边长为x厘米,矩形纸板的两边AB,BC的长分别为a厘米和b厘米,其中a≥b.
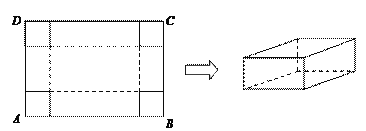
(1)当a=90时,求纸盒侧面积的最大值;
(2)试确定a,b,x的值,使得纸盒的体积最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于R上的可导函数f(x),若a>b>1且有(x﹣1)f′(x)≥0,则必有( )
A.f(a)+f(b)<2f(1)
B.f(a)+f(b)≤2f(1)
C.f(a)+f(b)≥2f(1)
D.f(a)+f(b)>2f(1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市2016年11月1日![]() 11月30日对空气污染指数的监测数据如下(主要污染物可吸入颗粒物):61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,83,82,82,64,79,86,85,75,71,49,45.
11月30日对空气污染指数的监测数据如下(主要污染物可吸入颗粒物):61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,83,82,82,64,79,86,85,75,71,49,45.
样本频率分布表:
分组 | 频数 | 频率 |
| 2 |
|
| 1 |
|
| 4 |
|
| 6 |
|
| 10 |
|
| ||
| 2 |
|
(Ⅰ)完成频率分布表;
(Ⅱ)作出频率分布直方图;
(Ⅲ)根据国家标准,污染指数在0![]() 50之间时,空气质量为优;在51
50之间时,空气质量为优;在51![]() 100之间时为良;在101
100之间时为良;在101![]() 150之间时,为轻微污染;在151
150之间时,为轻微污染;在151![]() 200之间时,为轻度污染.请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
200之间时,为轻度污染.请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com