
����Ŀ�����ڶ�����ΪI�ĺ���y=f��x���������������[m��n]I��ͬʱ���㣺
��f��x����[m��n]���ǵ���������
�ڵ���������[m��n]��f��x��ֵ��Ҳ��[m��n]�����[m��n]�Ǻ���y=f��x���ġ������䡱��
��1����g��x��=loga��ax��2a��+loga��ax��3a��������a��0��a��1������g��x���Ķ������ж��䵥���ԣ�
��2�����жϣ�1���е�g��x���Ƿ���ڡ������䡱����˵�����ɣ�
��3����֪����P��x��= ![]() ��t��R��t��0���С������䡱[m��n]����t�仯ʱ����n��m �����ֵ��
��t��R��t��0���С������䡱[m��n]����t�仯ʱ����n��m �����ֵ��
���𰸡�
��1���⣺�����⣺ ![]() ����ã�ax��3a��
����ã�ax��3a��
�ٵ�a��1ʱ��x��log3��3a����������ʱ������D=��log3��3a����+�ޣ���
��x1��x2��x1��x2��D��
�� ![]() ����0��
����0�� ![]() ��0��
��0�� ![]() ��
��
�� ![]() ��
�� ![]() ��
��
��g��x2����g��x1��
�ʵú���g��x���ڶ�����D=��log3��3a����+�ޣ�������������
�ڵ�0��a��1ʱ��x��log3��3a����������ʱ������D=�����ޣ�log3��3a������
ͬ����֤g��x���ڶ�����D=�����ޣ�log3��3a��������������
��2���⣺����g��x�����ڡ������䡱���ɣ�1����֪m��n��D��m��n��
���¶����У� ![]() ����x�ķ����ڶ�����D�����������ȵ�ʵ������
����x�ķ����ڶ�����D�����������ȵ�ʵ������
����ax��2a����ax��3a��=ax�ڶ�����D�����������ȵ�ʵ��������*��
��t=ax����*����t��2a����t��3a��=t����t2����5a+1��t+6a2=0�ڣ�3a��+�ޣ������������ȵ�ʵ������
��t2����5a+1��t+6a2=P��t����
�� 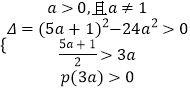 ����ã�a�⣮
����ã�a�⣮
���Ժ���g��x�������ڡ������䡱
��3���⣺�����裬����P��x��= ![]() =
= ![]() ��t��R��t��0���С������䡱[m��n]���䶨����Ϊ�����ޣ�0���ȣ�0��+�ޣ���
��t��R��t��0���С������䡱[m��n]���䶨����Ϊ�����ޣ�0���ȣ�0��+�ޣ���
��[m��n]�����ޣ�0����[m��n]��0��+�ޣ���
���ݷ����������ʣ�����P��x��= ![]() ��[n��m]�ϵ���������
��[n��m]�ϵ���������
�� ![]() ������m��n�Ƿ���p��x��=xʵ������
������m��n�Ƿ���p��x��=xʵ������
������t2x2����t2+t��x+1=0��ͬ�ŵ�����ʵ������
��mn= ![]() ��0��mnͬ�ţ�
��0��mnͬ�ţ�
���=��t2+t����4t2��0��t����3����ã�t��1��t����3��
m��n= ![]() ��
��
��t=3��n��m�����ֵ ![]()
����������1�����ݶ�������������0�������۵���a��1�Ĵ�С�ɵö�������֤�������ԣ���2�����ݶ�������[m��n]��f��x��ֵ��Ҳ��[m��n]��������ϵ���a��ֵ�����жϣ���3�����ݶ�������[m��n]��f��x��ֵ��Ҳ��[m��n]��������ϵ��ת��Ϊ���κ����������䷽�����ֵ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ΪR�ĺ���f��x������f��x+2��=2f��x������x��[0��2��ʱ��f��x��= 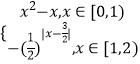 ����x��[��4����2��ʱ��f��x����
����x��[��4����2��ʱ��f��x���� ![]() ���������ʵ��t��ȡֵ��Χ�ǣ� ��
���������ʵ��t��ȡֵ��Χ�ǣ� ��
A.[��2��0���ȣ�0��1��
B.[��2��0����[1��+�ޣ�
C.[��2��1]
D.�����ޣ���2]�ȣ�0��1]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l�IJ������̣� 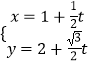 ��tΪ��������������ԭ��Ϊ���㣬x���������Ϊ���ᣬ��ȡ��ͬ�ij��ȵ�λ����������ϵ������C�ļ����귽��Ϊ��2=
��tΪ��������������ԭ��Ϊ���㣬x���������Ϊ���ᣬ��ȡ��ͬ�ij��ȵ�λ����������ϵ������C�ļ����귽��Ϊ��2= ![]() ��
��
��1��������C��ֱ�����귽�̺�ֱ��l����ͨ���̣�
��2��������C��ֱ��l����A��B���㣬��P��1��2������|PA|+|PB|��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
�� ![]() �����¶���ֱ�Ϊ
�����¶���ֱ�Ϊ![]() ���ҵ�
���ҵ�![]() ��
�� ![]() �ֱ�Ϊ��Բ
�ֱ�Ϊ��Բ![]() �����ҽ��㣬��
�����ҽ��㣬��![]() ��
��
��������Բ![]() �ı����̣�
�ı����̣�
������![]() ����Բ������
����Բ������![]() ��
�� ![]() ������һ�㣬����
������һ�㣬����![]() ��
��![]() ����
����![]() ��
�� ![]() Ϊ�߶�
Ϊ�߶�![]()
���е㣮ֱ��![]() ��ֱ��
��ֱ��![]() ���ڵ�
���ڵ�![]() ��
�� ![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬
���е㣬 ![]() Ϊ����ԭ�㣮��
Ϊ����ԭ�㣮��
![]() �Ĵ�С��
�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x2+mx+n��������㩁1��3��
��1���������f��x���Ľ���ʽ����ָ������f��x���ĵ����������䣻
��2����g��x��=f��|x|����x1 �� x2��[t��t+1]������������ʵ��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �������ڳ���
�������ڳ���![]() ��ʹ�ö�����
��ʹ�ö�����![]() ������
������![]() �����
�����![]() Ϊ�н缯�ϣ�ͬʱ��
Ϊ�н缯�ϣ�ͬʱ��![]() Ϊ����
Ϊ����![]() ���Ͻ磮
���Ͻ磮
��1����![]() ��
��![]() �����ж�
�����ж�![]() ��
��![]() �Ƿ�Ϊ�н缯�ϣ���˵�����ɣ�
�Ƿ�Ϊ�н缯�ϣ���˵�����ɣ�
��2����֪![]() ����
����![]() ��
��![]() ������
������![]() ��
��
![]() ����
����![]() Ϊ�н缯�ϣ���
Ϊ�н缯�ϣ���![]() ��ֵ��
��ֵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����![]() ����������
��Ϊ��������![]() �е���С����Ϊ
�е���С����Ϊ![]() ���Ƿ��������
���Ƿ��������![]() ��ʹ��
��ʹ��![]() Ϊ�н缯��
Ϊ�н缯��![]() ��
�� ![]() ������
��Ϊ����![]() ���Ͻ磬�����ڣ�����
���Ͻ磬�����ڣ�����![]() ����Сֵ���������ڣ���˵�����ɣ�
����Сֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��ֵ��Ϊ����A������x�IJ���ʽ
��ֵ��Ϊ����A������x�IJ���ʽ ![]() �Ľ⼯ΪB������
�Ľ⼯ΪB������ ![]() ������D={x|m+1��x��2m��1}��m��0��
������D={x|m+1��x��2m��1}��m��0��
��1����A��B=B����ʵ��a��ȡֵ��Χ��
��2����DC����ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ABCD��A1B1C1D1���������ı���ABCDΪ������A1A��AB��2����ABC��![]() ��E��F�ֱ���BC��A1C���е���
��E��F�ֱ���BC��A1C���е���
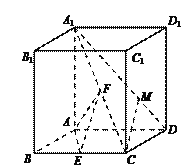
��1��������ֱ��EF��AD���ɽǵ�����ֵ��
��2����M���߶�A1D�ϣ� ![]() ����CM��ƽ��AEF����ʵ������ֵ��
����CM��ƽ��AEF����ʵ������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��=ax��lnx��x�ʣ�0��e]��g��x��= ![]() ������e����Ȼ������a��R��
������e����Ȼ������a��R��
��1������a=1ʱ������f��x���ĵ����Ժͼ�ֵ��
��2����֤���ڣ�1���������£�f��x����g��x��+ ![]() ��
��
��3���Ƿ����ʵ��aʹf��x������Сֵ��3�������ڣ����a��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com